Question 2 (12 marks) Use a SEPARATE writing booklet. (a) Let $f(x) = \sin^{-1}(x + 5)$. (i) State the domain and range of the function $f(x)$. (ii) Find the gradient of the graph of $y = f(x)$ at the point where $x = -5$. (iii) Sketch the graph of $y = f(x)$. (b) (i) By applying the binomial theorem to $(1 + x)^{n}$ and differentiating, show that $$n(1 + x)^{n - 1} = \binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^{2} + \ldots + \binom{n}{n}x^{n-1}$$ (ii) Hence deduce that $$n3n-1 = \binom{n}{0} + \binom{n}{1}r + \ldots + \binom{n}{n}2n^{n}$$ Question 2 continued (c) The points $P(2ap, aq^{2}), Q(2aq, aq^{2})$ and $R(2ar, ar^{2})$ lie on the parabola $x^{2} = 4ay$. The chord $QR$ is perpendicular to the axis of the parabola. The chord $PR$ meets the axis of the parabola at $U$. The equation of the chord $PR$ is $y = \frac{1}{2}(p + r)x - apr$. The equation of the tangent at $P$ is $y = px - aq^{2}$. (i) Find the coordinates of $U$. (ii) The tangents at $P$ and $Q$ meet at the point $T$. Show that the coordinates of $T$ are $(a(p + q), aq)$. (iii) Show that $TU$ is perpendicular to the axis of the parabola.

SSCE HSC Mathematics Extension 1 Differentiation of inverse trigonometric functions: Question 2 (12 marks) Use a SEPA

Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1

Question 2

Question 2 (12 marks) Use a SEPARATE writing booklet. (a) Let $f(x) = \sin^{-1}(x + 5)$. (i) State the domain and range of the function $f(x)$. (ii) Find the gradi... show full transcript

Worked Solution & Example Answer:Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1

Step 1

Let $f(x) = \sin^{-1}(x + 5)$. (i) State the domain and range of the function $f(x)$.

96%

114 rated

Answer

The function $f(x) = \sin^{-1}(x + 5)$ is defined when the argument of $\sin^{-1}$ lies within the interval [-1, 1]. Therefore, we set:

$-1 \leq x + 5 \leq 1$

Solving for $x$ gives:

$-6 \leq x \leq -4$

Thus, the domain of $f(x)$ is $[-6, -4]$ .

The range of $f(x)$ is the output values of the inverse sine function, which are:

$\left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$

Step 2

(ii) Find the gradient of the graph of $y = f(x)$ at the point where $x = -5$.

99%

104 rated

Answer

To find the gradient, we need to differentiate the function $f(x) = \sin^{-1}(x + 5)$ :

$f'(x) = \frac{1}{\sqrt{1 - (x + 5)^{2}}}$

Now, we evaluate at the point $x = -5$ :

$f'(-5) = \frac{1}{\sqrt{1 - (-5 + 5)^{2}}} = \frac{1}{\sqrt{1 - 0}} = 1$

Thus, the gradient at $x = -5$ is 1.

Step 3

(iii) Sketch the graph of $y = f(x)$.

96%

101 rated

Answer

To sketch the graph, plot the points at the boundaries of the domain $[-6, -4]$ .

For $x=-6$ , $f(-6)=\sin^{-1}(-1)= -\frac{\pi}{2}$
For $x=-4$ , $f(-4)=\sin^{-1}(1)=\frac{\pi}{2}$

Connect these points smoothly, noting the general shape of $\sin^{-1}$ , and label the axes and points.

Step 4

(b) (i) By applying the binomial theorem to $(1 + x)^{n}$ and differentiating, show that

98%

120 rated

Answer

By the binomial theorem, we have:

$(1 + x)^{n} = \sum_{k=0}^{n} \binom{n}{k} x^{k}$

Differentiating both sides with respect to $x$ gives:

$n(1 + x)^{n - 1} = \sum_{k=1}^{n} k \binom{n}{k} x^{k - 1}$

This shows the relationship, confirming the term contributions.

Step 5

(ii) Hence deduce that

97%

117 rated

Answer

Using our previous result, we can state:

$n3^{n-1} = \sum_{k=0}^{n} \binom{n}{k} r^{k} \cdot (2^{n - k})$

This represents the total counts, deriving from the binomial expansions.

Step 6

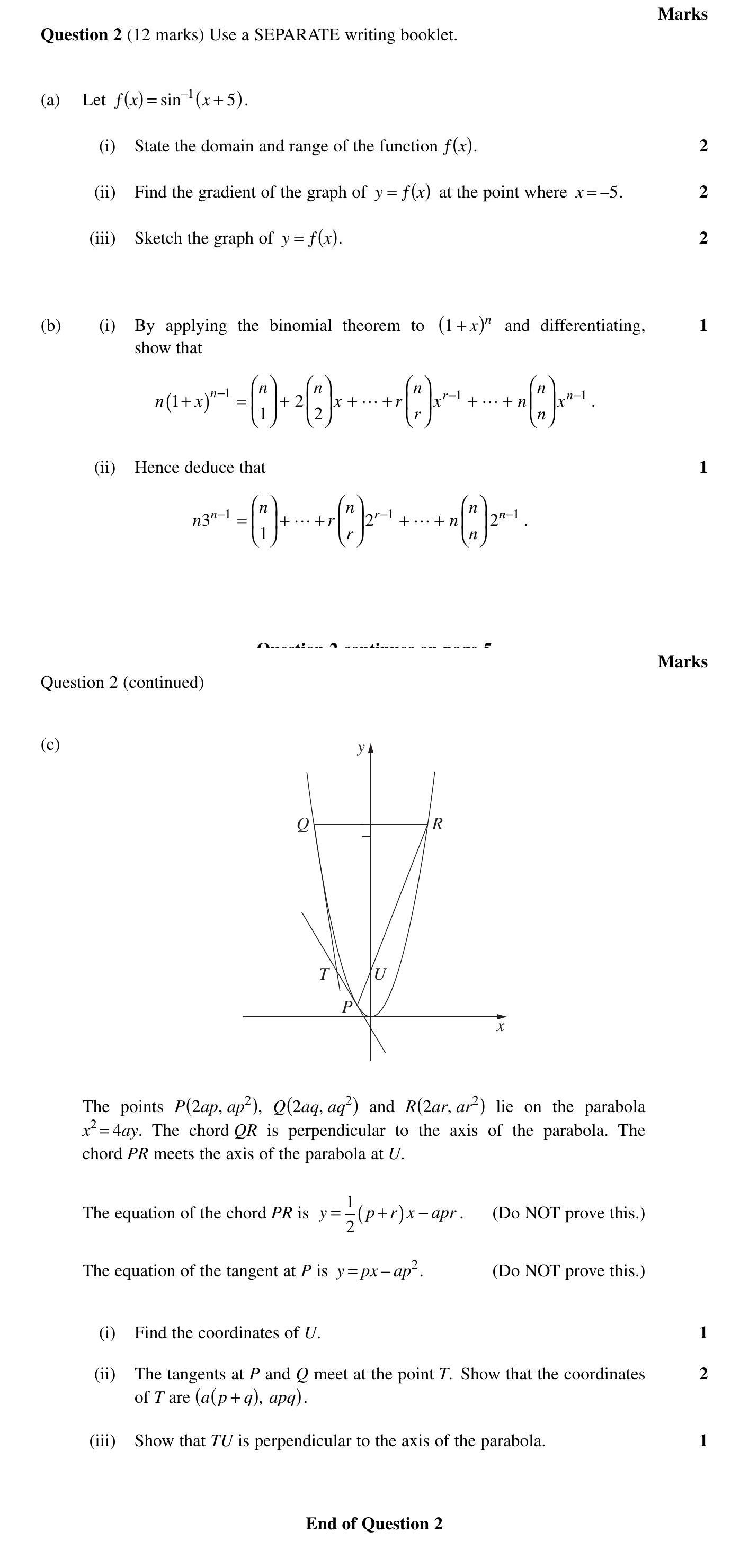
(c) (i) Find the coordinates of $U$.

97%

121 rated

Answer

Finding the coordinates of point $U$ requires utilizing the equations of the chords and the parabolic property. Set the equations accordingly to find the intersection with the x-axis.

The solution will depend on manipulating the provided information.

Step 7

(ii) The tangents at $P$ and $Q$ meet at the point $T$. Show that the coordinates of $T$ are $(a(p + q), aq)$.

96%

114 rated

Answer

Calculate the intersection of the two tangent lines at $P$ and $Q$ . Setting equal the equations:

$y = \frac{1}{2}(p + r)x - apr$

By substituting and simplifying, find that $T = (a(p + q), aq)$ .

Step 8

(iii) Show that $TU$ is perpendicular to the axis of the parabola.

99%

104 rated

Answer

To show perpendicularity, verify that the product of the slopes of lines $TU$ and the axis equals -1. This can be investigated via coordinate changes leading to the slope ratios.

Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1

Worked Solution & Example Answer:Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1

Let $f(x) = \sin^{-1}(x + 5)$. (i) State the domain and range of the function $f(x)$.

(ii) Find the gradient of the graph of $y = f(x)$ at the point where $x = -5$.

(iii) Sketch the graph of $y = f(x)$.

(b) (i) By applying the binomial theorem to $(1 + x)^{n}$ and differentiating, show that

(ii) Hence deduce that

(c) (i) Find the coordinates of $U$.

(ii) The tangents at $P$ and $Q$ meet at the point $T$. Show that the coordinates of $T$ are $(a(p + q), aq)$.

(iii) Show that $TU$ is perpendicular to the axis of the parabola.

Join the SSCE students using SimpleStudy...