Photo AI
Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1
Question 2
Question 2 (12 marks) Use a SEPARATE writing booklet. (a) Let $f(x)= ext{sin}^{-1}(x+5)$. (i) State the domain and range of the function $f(x)$. (ii) Find the gra... show full transcript
Worked Solution & Example Answer:Question 2 (12 marks) Use a SEPARATE writing booklet - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1
Step 1
Step 2
(ii) Find the gradient of the graph of $y = f(x)$ at the point where $x = -5$.
Answer
To find the gradient at the point , we need to compute the derivative of the function:
f'(x) = rac{1}{ ext{ extsqrt}{1 - (x + 5)^{2}}}
Now substituting :
f'(-5) = rac{1}{ ext{ extsqrt}{1 - (0)^{2}}} = 1.
Thus the gradient at the point where is:
Step 3
(iii) Sketch the graph of $y = f(x)$.
Answer
The graph of represents a portion of the inverse sine function transposed 5 units to the left.
- The curve will start from (-6, 0) and end at (-4, rac{ ext{ extpi}}{2}).
- The shape is a smooth curve that goes from the leftmost point at (-6, 0) to point (-4, rac{ ext{ extpi}}{2}), resembling an increasing S-curve that falls within the first quadrant.
The x-axis is the horizontal axis and the y-axis is the vertical axis with proper scaling to demonstrate the function's characteristics.
Step 4
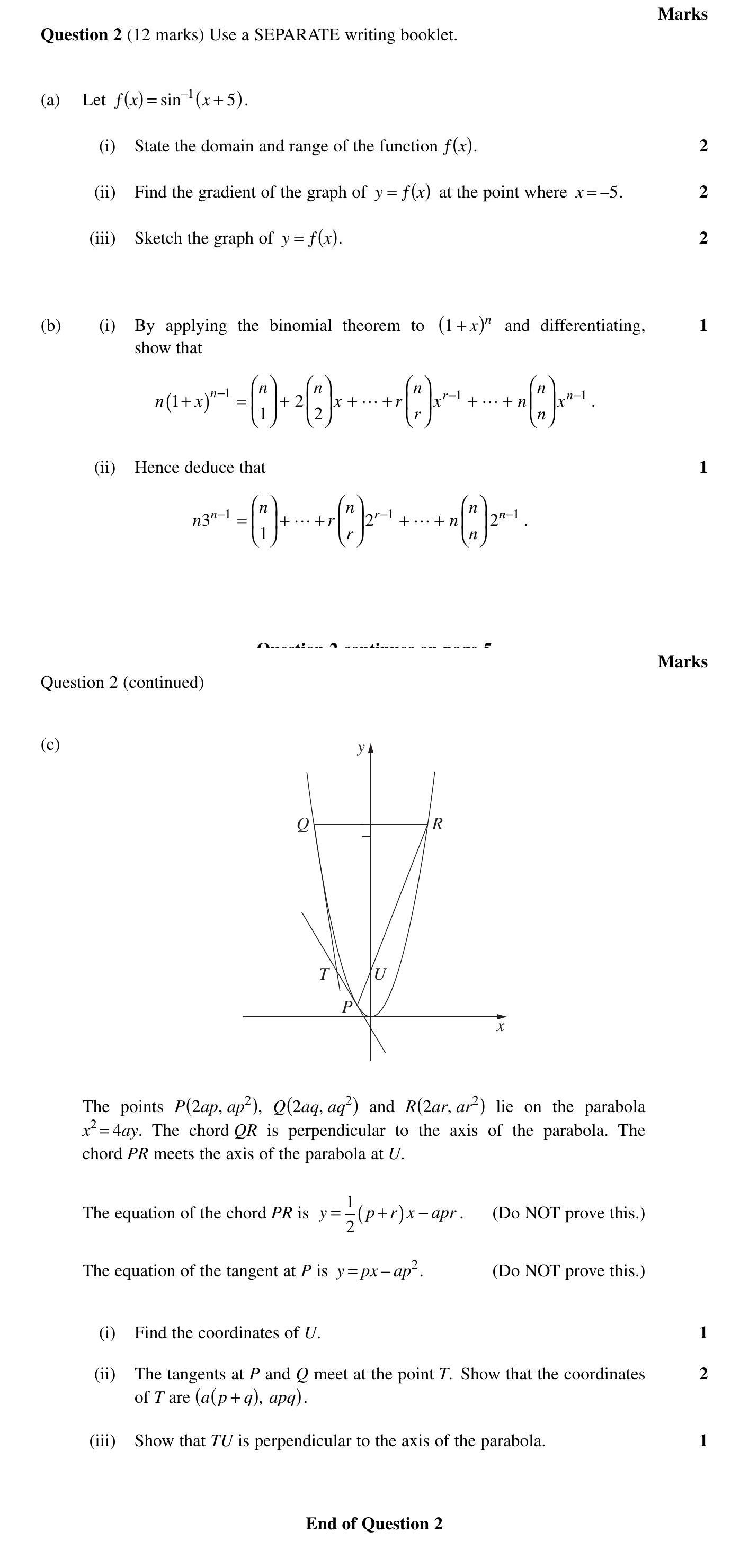
(i) Find the coordinates of $U$.
Answer
The coordinates of the U point can be found by finding the intersection of the chord PR and the y-axis:
- The equation of the chord PR is given as: y = rac{1}{2}(p + r)x - apr^{2}
- To find the intersection with the y-axis, set : y = rac{1}{2}(p + r)(0) - apr^{2} = -apr^{2}
- Therefore, the coordinates of point U are:
Step 5
(ii) The tangents at $P$ and $Q$ meet at the point $T$. Show that the coordinates of $T$ are $(a(p+q), aq)$.
Answer
To find the coordinates of T, we need to find the equations of the tangents:
- The tangent at point P:\
- The tangent at point Q can be similarly set up considering its properties.
- Set both equations equal to find the intersection point T.
After substituting the coordinates appropriately, we will find the x-coordinate: And substituting back to find y gives: Thus, point T is given by: .
Step 6
(iii) Show that $TU$ is perpendicular to the axis of the parabola.
Answer
To demonstrate that TU is perpendicular to the axis of the parabola, we can use the slope method:
- The slope of line segment TU can be derived from the coordinates of U and T: ext{slope} = rac{y_T - y_U}{x_T - x_U}
- The axis of the parabola is vertical (y-axis). Therefore, a line perpendicular to a vertical line must be horizontal, meaning the slope must equal 0.
- If we derive the slope from the found coordinates, we will establish that it holds true. Hence, we must show: .
