Photo AI
(a) Let $f(x) = \sin^{-1}(x + 5)$ - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1
Question 2
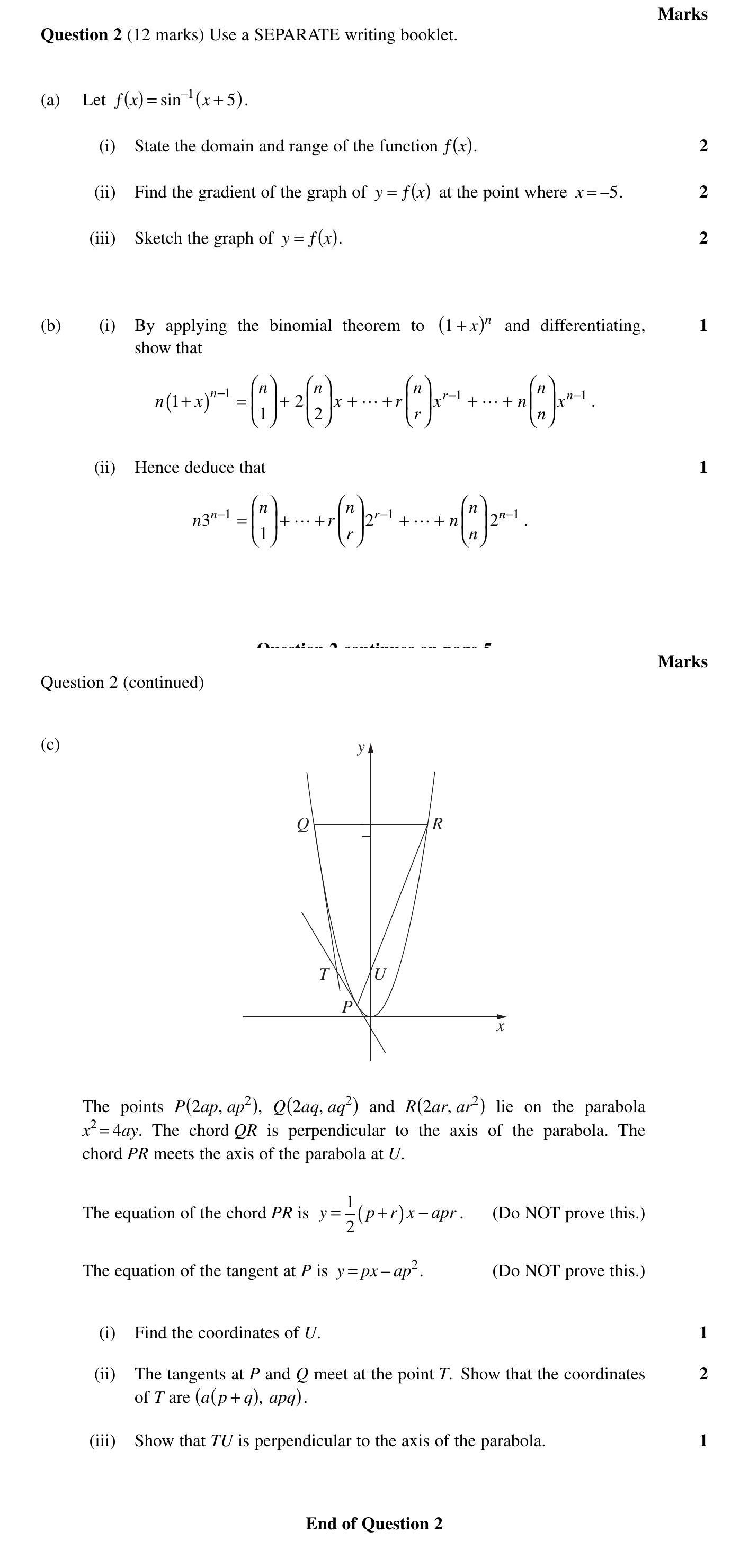
(a) Let $f(x) = \sin^{-1}(x + 5)$. (i) State the domain and range of the function $f(x)$. (ii) Find the gradient of the graph of $y = f(x)$ at the point ... show full transcript
Worked Solution & Example Answer:(a) Let $f(x) = \sin^{-1}(x + 5)$ - HSC - SSCE Mathematics Extension 1 - Question 2 - 2006 - Paper 1
Step 1
State the domain and range of the function $f(x)$
Answer
The function has a domain given by the constraint that the argument of must lie between -1 and 1. Hence, we have the inequality:
This simplifies to:
Thus, the domain of is . The range of is given by the outputs of the function for the input values within this domain, which yields the range .
Step 2
Step 3
Step 4
Step 6
Find the coordinates of $U$
Answer
To find the coordinates of the point , we know that the chord can be expressed in terms of its endpoints, which are points on the parabola. Since is perpendicular to the axis of the parabola, it would intersect the y-axis vertically. We need to plug the necessary values for in terms of to find the coordinates.
Step 7
The tangents at $P$ and $Q$ meet at the point $T$. Show that the coordinates of $T$ are $(a(p + q), aqp)$
Answer
To show this, we will calculate the slopes of the tangents at points and . The equations of the tangents are:
Setting these two equations equal will yield the coordinates of point .
Step 8
Show that $TU$ is perpendicular to the axis of the parabola
Answer
To demonstrate that line segment is perpendicular to the axis of the parabola, we must investigate the slopes of the segments and the axis. If the product of their slopes is , this will confirm that they are indeed perpendicular.
