Photo AI
Given that \( \overrightarrow{OP} = \begin{pmatrix} -3 \\ 1 \end{pmatrix} \) and \( \overrightarrow{OQ} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} \), what is \( \overrightarrow{PQ} \? - HSC - SSCE Mathematics Extension 1 - Question 1 - 2021 - Paper 1
Question 1
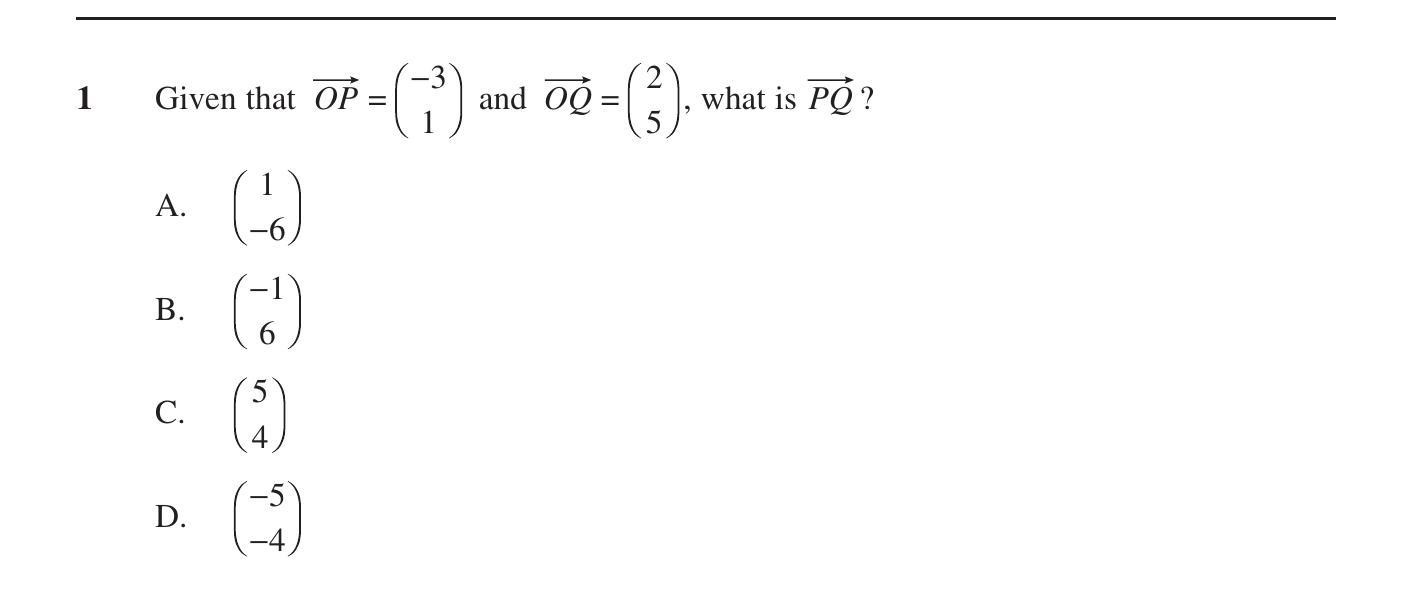
Given that \( \overrightarrow{OP} = \begin{pmatrix} -3 \\ 1 \end{pmatrix} \) and \( \overrightarrow{OQ} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} \), what is \( \overr... show full transcript
Worked Solution & Example Answer:Given that \( \overrightarrow{OP} = \begin{pmatrix} -3 \\ 1 \end{pmatrix} \) and \( \overrightarrow{OQ} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} \), what is \( \overrightarrow{PQ} \? - HSC - SSCE Mathematics Extension 1 - Question 1 - 2021 - Paper 1
Step 1
