Photo AI

There are two tanks on a property, Tank A and Tank B - HSC - SSCE Mathematics Standard - Question 24 - 2020 - Paper 1

Question icon

Question 24

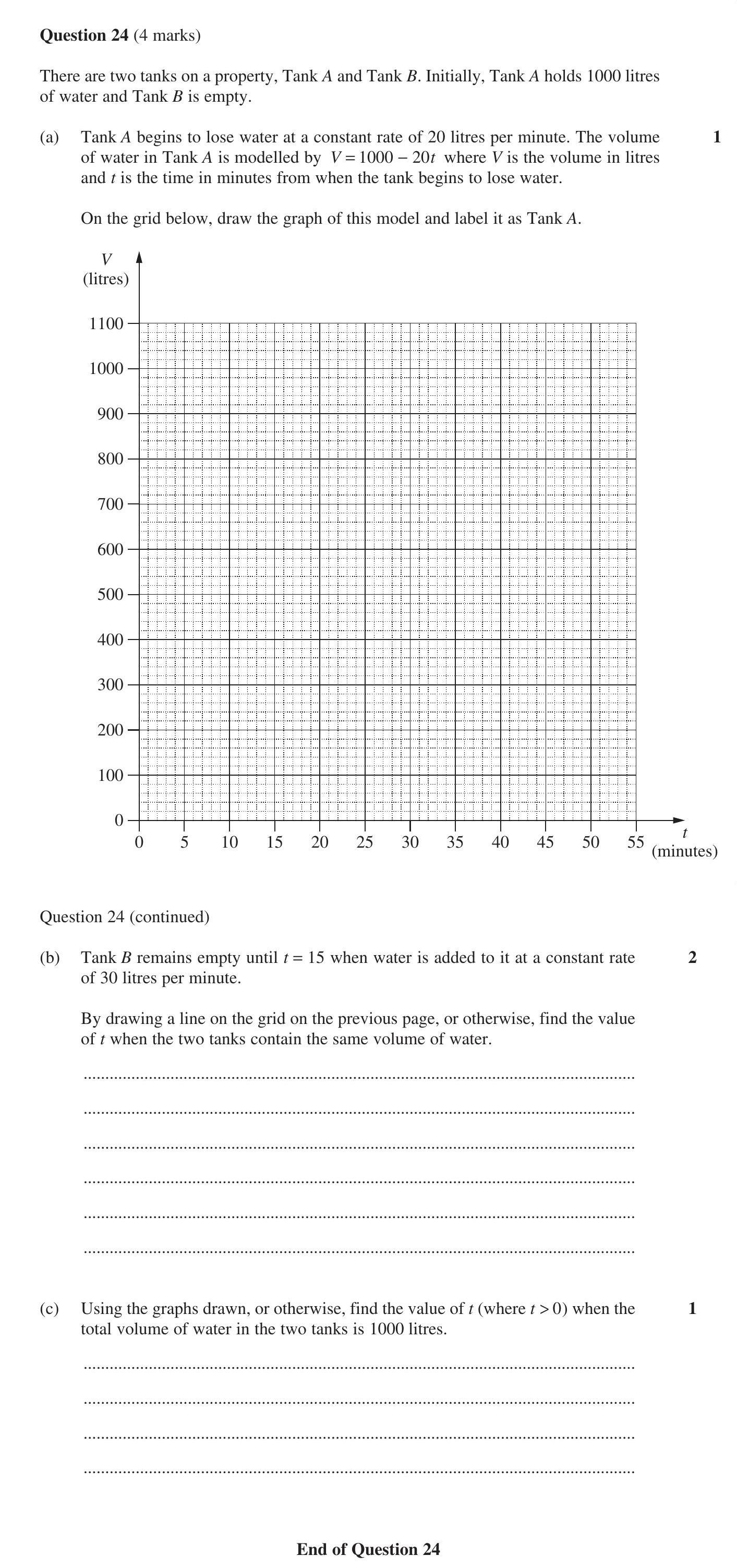
There-are-two-tanks-on-a-property,-Tank-A-and-Tank-B-HSC-SSCE Mathematics Standard-Question 24-2020-Paper 1.png

There are two tanks on a property, Tank A and Tank B. Initially, Tank A holds 1000 litres of water and Tank B is empty. (a) Tank A begins to lose water at a constan... show full transcript

Worked Solution & Example Answer:There are two tanks on a property, Tank A and Tank B - HSC - SSCE Mathematics Standard - Question 24 - 2020 - Paper 1

Step 1

a) Draw the graph of Tank A

96%

114 rated

Answer

To draw the graph of Tank A, we can use the equation V=1000−20tV = 1000 - 20t. This means that for each minute that passes, 20 litres are lost from the initial 1000 litres.

  1. At t=0t = 0, V=1000V = 1000 litres.
  2. At t=10t = 10, V=800V = 800 litres.
  3. At t=20t = 20, V=600V = 600 litres.
  4. At t=25t = 25, V=500V = 500 litres.
  5. At t=50t = 50, V=0V = 0 litres (the tank would be empty).

Plot these points on the graph and connect them to show a straight line decreasing from (0, 1000) to (50, 0). Label this line as 'Tank A'.

Step 2

b) Find the value of $t$ when tanks are the same volume

99%

104 rated

Answer

Tank B starts filling at t=15t = 15 minutes.

  1. From t=15t = 15, the volume of Tank B can be calculated as VB=30(t−15)V_B = 30(t - 15) once it starts filling.

  2. To find when both tanks are equal, set the equations equal: 1000−20t=30(t−15)1000 - 20t = 30(t - 15).

  3. Rearranging gives:

    1000 - 20t = 30t - 450

    1450 = 50t

    t = rac{1450}{50} = 29.

The two tanks contain the same volume at t=29t = 29 minutes.

Step 3

c) Find $t$ when total volume is 1000 litres

96%

101 rated

Answer

To find when the total volume in both tanks is 1000 litres:

  1. The total volume is VA+VB=1000V_A + V_B = 1000 litres.

  2. From part (a), VA=1000−20tV_A = 1000 - 20t and from part (b), VB=30(t−15)V_B = 30(t - 15) for textext15t ext{ } ext{ } 15.

  3. Setting up the equation:

    (1000 - 20t) + 30(t - 15) = 1000

    Simplifying: 1000 - 20t + 30t - 450 = 1000

    10t - 450 = 0

    t = 45.

At t=45t = 45 minutes, the total volume of water in the two tanks is 1000 litres.

Join the SSCE students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;