Two right-angled triangles, ABC and ADC, are shown - HSC - SSCE Mathematics Standard - Question 22 - 2019 - Paper 1

Question 22
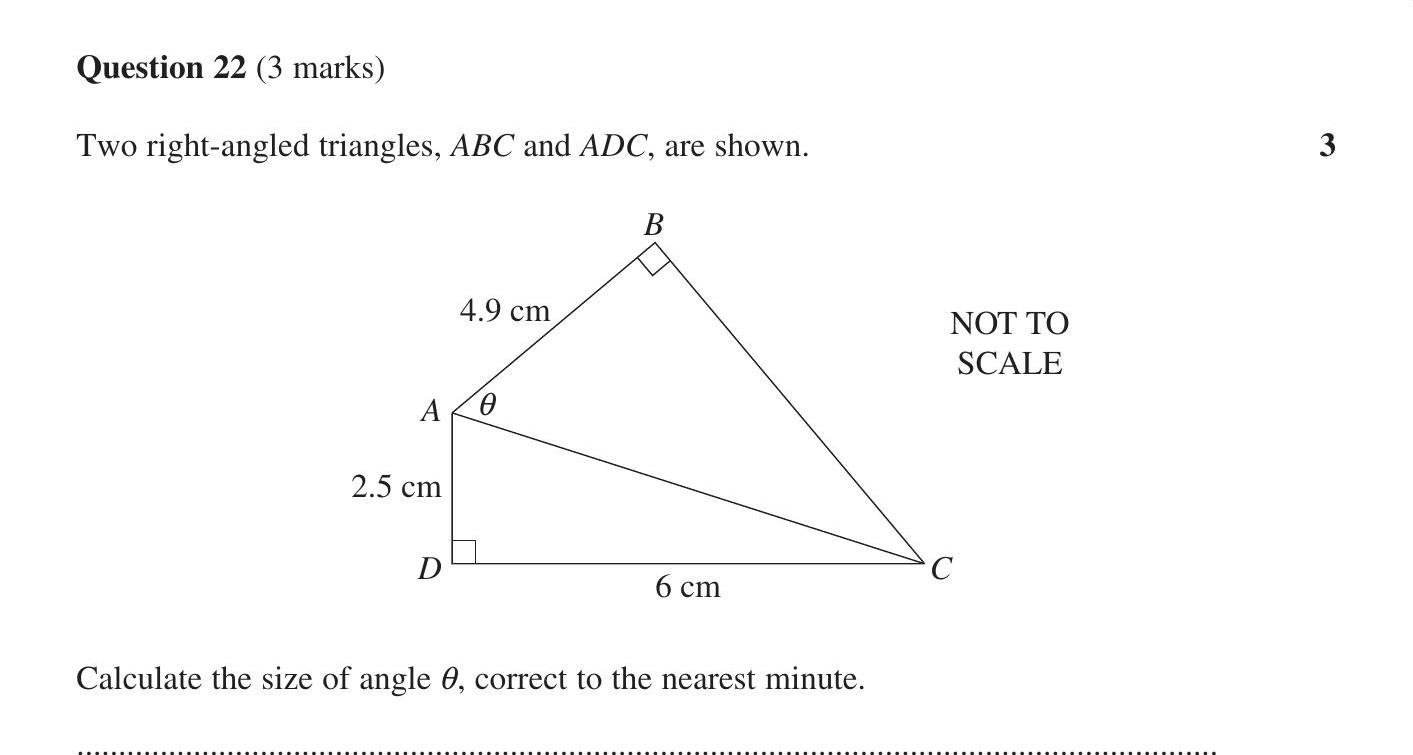
Two right-angled triangles, ABC and ADC, are shown.
Calculate the size of angle $\theta$, correct to the nearest minute.
Worked Solution & Example Answer:Two right-angled triangles, ABC and ADC, are shown - HSC - SSCE Mathematics Standard - Question 22 - 2019 - Paper 1
Calculate AC

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Using the Pythagorean theorem:
AC2=AD2+DC2
Substituting the values:
AC2=(2.5)2+(6)2
Calculating:
AC2=6.25+36=42.25
Thus, taking the square root:
AC=42.25=6.5 cmUse the cosine ratio to find $\theta$

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Using the cosine ratio:
cos(θ)=HypotenuseAdjacent=6.54.9
Calculating:
cos(θ)=0.754≈0.754
Now, to find the angle θ:
θ=cos−1(0.754)
Using a calculator, we find:
θ≈41.075∘Round to the nearest minute

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
The decimal part, 0.075 times 60 gives approximately 4.5 minutes. Therefore, rounding gives:
θ≈41∘5′Join the SSCE students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered

