Photo AI
Last Updated Sep 24, 2025
Understanding Angles of Any Magnitude Simplified Revision Notes for SSCE HSC Mathematics Advanced
Revision notes with simplified explanations to understand Understanding Angles of Any Magnitude quickly and effectively.
409+ students studying
Understanding Angles of Any Magnitude
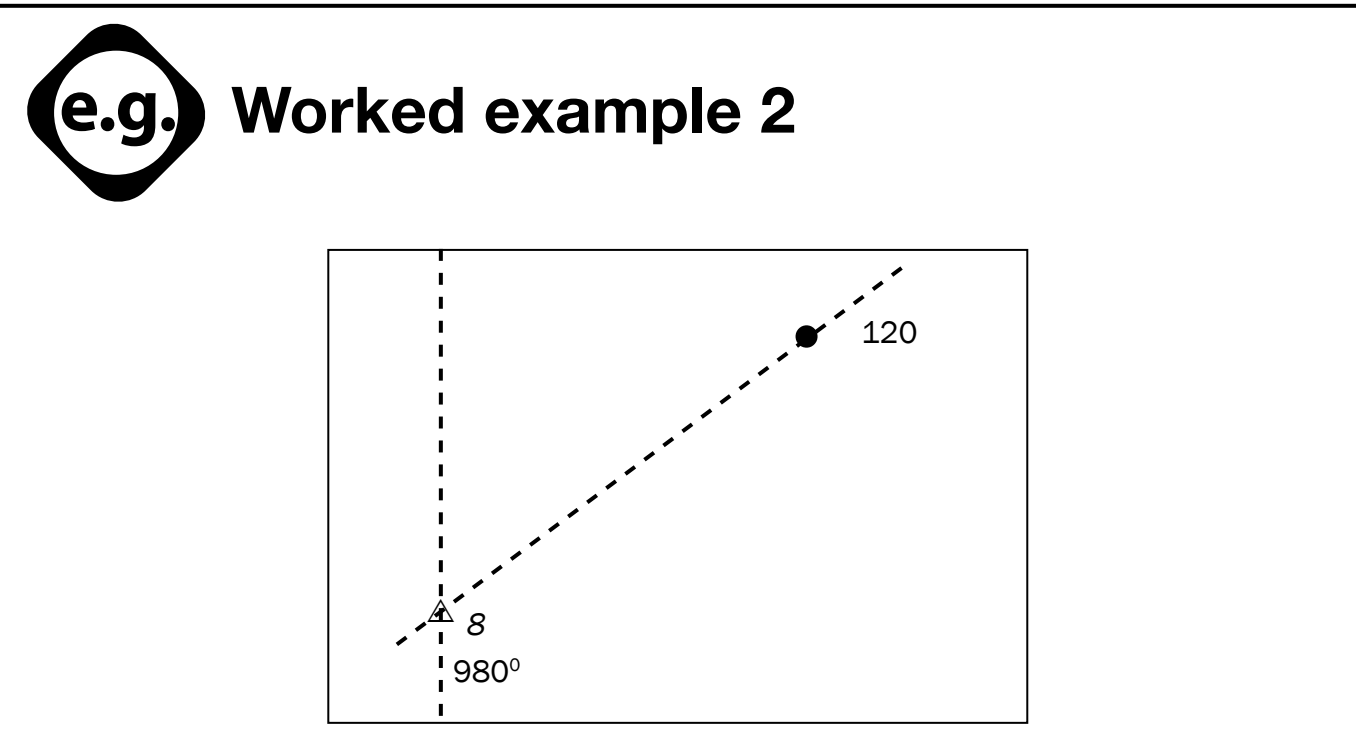
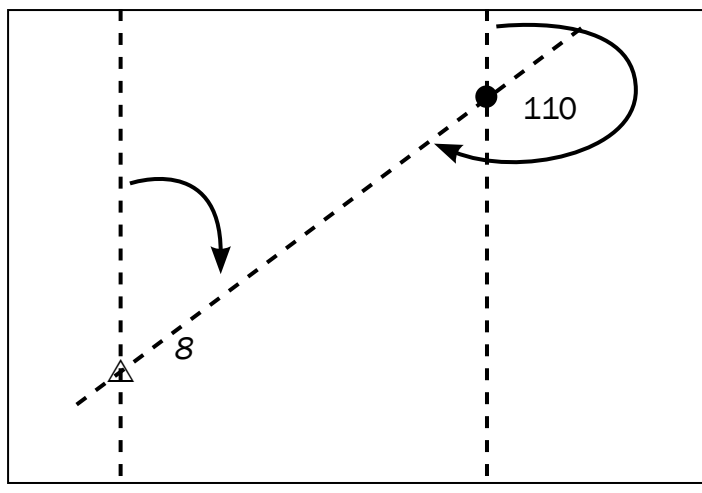
Introduction to Angles Beyond 360°/2π
- Definition: Angles beyond a complete rotation surpass the full cycle of 360° or radians. They are considered positive when measured counter-clockwise and negative if measured clockwise.
Angles of Any Magnitude: Angles extending beyond a full rotation, such as 360° or radians.
- Relevance:
- Integral for advanced mathematical fields, pivotal in engineering and physics.
- Crucial in calculating periodic functions and rotations within mechanical systems.
Misconceptions and Clarifications
-
Common Misconceptions:
-
Degrees:
- Negative angles signify clockwise rotation. Example: -45° means a 45° rotation clockwise.
-
Radians:
- Often perceived as less intuitive but are vital for calculus concepts.
infoNoteConversion Strategy: Practise conversions with the equivalence radians. For example:
-
-
Visual Aids: Diagrams integrated to explain positive and negative angle progression.
Utilisation of the Unit Circle
-
Understanding the Unit Circle:
- Shows that angles can extend beyond a single rotation.
- Clearly displays positions in both radians and degrees.
-
Example Walkthrough:
- Angle represents two full rotations, equivalent to or radians.
- Conversion:
Integration of Visual Aids
-
Additional Diagrams and Descriptions:
- Illustrate conversion processes visually on the unit circle.
- Include concise 'Key Takeaway' notes for transformations.
-
Visual Focus:
- Use colour-coding for angles to emphasise standard (0-360°) versus extended cycles.
Conversion Between Degrees and Radians
Introduction
- Converting between degrees and radians is fundamental in trigonometry, engineering, and navigation.
- These measurements are critical in angle calculations for design, navigation systems, and wave equations.
Conversion Formulas
- Degrees to Radians: Radians = Degrees
- Radians to Degrees: Degrees = Radians
Degrees: The basic unit for angle measurement, with a complete circle equalling 360°.
Detailed Example Problems with Solutions
Example 1: Converting Degrees to Radians
- Given: 45°
- Use Formula: Radians = Degrees
- Substitute: Radians = 45
- Simplify: Radians =
Common Error: Always include in radian calculations!
Example 2: Converting Radians to Degrees
- Given: radians
- Use Formula: Degrees = Radians
- Substitute: Degrees =
- Simplify: Degrees = 45°
Remember: Ensure is appropriately cancelled when converting to degrees.
Highlighting Common Pitfalls
- Forgetting : Never omit in conversions.
- Calculator Errors:
- Set the calculator accurately to degree or radian mode.
- Double-check settings before solving problems.
Calculator Mode Importance
- Correct Mode Setting:
- Ensure calculators are in either DEG or RAD mode according to the problem context.
- Incorrect modes can lead to significant errors.
Mode Settings: Validate that the calculator mode aligns with the problem requirements!
Understanding Periodicity
- Periodicity: Trigonometric functions repeat their values at specific intervals.
- Period Examples:
- Sine and Cosine repeat every 360° or radians.
- Tangent repeats every 180° or radians.
Analogies aid in depicting repetition. For instance:
- Clock face cycles, recurring every 12 hours, similar to how sine and cosine repeat every 360°.
- Seasonal cycles depict periodic natural occurrences.
Graphical Representation of Periodicity
-
Graphs of Sine and Cosine:
- Visual aids demonstrate amplitude and period.
- Observing how curves ascend or descend can help in understanding graph trends.
-
Tangent Graph:
- Tangent differs with vertical asymptotes.
- Students are encouraged to sketch or trace graphs for enhanced understanding.
Symmetry in Trigonometric Functions
- Odd and Even Functions:
- , indicating sine as odd.
- , identifying cosine as even.
- , denoting tangent as odd.
Odd Function: Symmetric about the origin. Even Function: Symmetric about the y-axis. Context: Aids in simplifying calculations across cycles, with predictive power in physics or engineering.
Key Trigonometric Identities
Overview of Trigonometric Identities
- Trigonometric identities: Equations involving trigonometric functions that universally apply.
- Importance: They simplify mathematical operations and efficiently solve trigonometric equations.
- Key Point: Allow transformation of complex expressions into easier forms.
- Historical Context:
- Hipparchus: Initiated creation of trigonometric tables.
- Ptolemy: Further developed these principles for broader applications.
List of Important Identities
-
Reciprocal Identities:
-
Quotient Identities:
-
Pythagorean Identities:
Positive and negative angles: Particular identities such as are significant.
Derivation and Explanation of Key Identities
Unit Circle
- Coordinates: and accord with points on a unit circle.
- Pythagorean Identity Derivation:
- Utilises , from .
Periodicity and Symmetry
- Periodicity: Patterns repeat every radians for and .
- Symmetry:
- Sine: An odd function, .
- Cosine: An even function, .
Significance in Simplifying Complex Problems
- Problem Example: Illustrate simplification of .
- Step 1: Start from .
- Step 2: Divide each term by : .
Expanded Problem-Solving Section
-
Worked Example:
- Method: Simplify using identity .
- Solution: .
-
Practice Problem:
- Simplify: .
- Tip: Employ the identity .
- Solution:
Consistency in sign usage is vital. Verify even and odd functions to avoid mistakes.
Problem Solving Techniques
Common Problem Types
-
Simplifying Expressions: Use periodic identities to simplify expressions.
Example: Simplify .
- Recognise periodic nature: .
-
Solving Trigonometric Equations:
- Example Walkthrough: Solve .
- Principal Value: .
- General Solution: , .
Step-by-Step Guides
-
Example 1: Convert an angle using modulo operation.
- Degrees: .
- Radians: .
-
Example 2: Solve using identities such as the Pythagorean identity.
- Walkthrough:
- Given .
- Use identity .
- Solve: .
- Walkthrough:
Using the Calculator Effectively
- Best Practices:
- Ensure calculators are correctly set (DEG/RAD).
- Tip: Always verify your calculator's settings.
- Validation: Double-check solutions.
Ensure accuracy across cycles using computational tools.
Common Pitfalls and Solutions
-
Pitfalls:
- Calculator mode setting errors.
- Misinterpreting periodic angles.
-
Call-Out Solutions:
Focus on correct mode and sign conventions beyond the initial cycle.
Graphical Understanding
Graphical Behaviour
-
Periodicity:
- Recognising repeat patterns is essential in trigonometry.
- Concepts:
-
Extended Graphs:
- Symmetry: Reflection or rotation can affect graph patterns.
- Phase Shifts: Influence of phase shifts on repeating and understanding graphs.
-
Key Transformations:
- Effective transformation clarifications:
- Vertical Shifts: Moves graph up or down.
- Horizontal Stretches: Widens or narrows graph.
- Reflections: Mirrors graph across axes.
- Effective transformation clarifications:
-
Annotated Graphs:
-
Axes Intersections: Crucial for understanding angle properties.
-
Maxima and Minima: Key points shown in diagrams.
Diagrams
500K+ Students Use These Powerful Tools to Master Understanding Angles of Any Magnitude For their SSCE Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Understanding Angles of Any Magnitude
Revise key concepts with interactive flashcards.
Try Mathematics Advanced Flashcards4 quizzes
Quizzes on Understanding Angles of Any Magnitude
Test your knowledge with fun and engaging quizzes.
Try Mathematics Advanced Quizzes29 questions
Exam questions on Understanding Angles of Any Magnitude
Boost your confidence with real exam questions.
Try Mathematics Advanced Questions27 exams created
Exam Builder on Understanding Angles of Any Magnitude
Create custom exams across topics for better practice!
Try Mathematics Advanced exam builder5 papers
Past Papers on Understanding Angles of Any Magnitude
Practice past papers to reinforce exam experience.
Try Mathematics Advanced Past PapersOther Revision Notes related to Understanding Angles of Any Magnitude you should explore
Discover More Revision Notes Related to Understanding Angles of Any Magnitude to Deepen Your Understanding and Improve Your Mastery
Load more notes