Exponential Functions Applications

Introduction

Exponential functions: are characterized by expressions in the form of $f(x) = a^x$, where $a > 0$. These functions hold substantial importance in various real-world scenarios such as finance, biology, and technology.

• Finance Example: Applied to compound interest calculations, demonstrating how wealth accumulates over time.
• Biology Example: Utilised in population growth models, depicting rapid increases in population sizes.
• Technology Example: Used in radioactive decay processes, depicting how material reduces over time.

Objectives

• Equip students with a strong comprehension of solving exponential equations.
• Demonstrate the extensive applications of exponential functions to enhance comprehension.

Key Properties

• Domain: All real numbers $(-\infty, \infty)$.
• Range: Positive real numbers $(0, \infty)$.
• Behaviour: Exponential functions exhibit a horizontal asymptote at the x-axis.

Graphical Representation

A diagram showcases exponential growth and decay:

• The curve intersects the point $(0, 1)$ since for any base $a^0 = 1$.
• As $x \to -\infty$, the graph nears the x-axis.
• As $x \to \infty$, growth functions escalate indefinitely, while decay functions converge towards zero.

Exponential Growth vs. Exponential Decay

Exponential Growth

• Characteristics: Rapid escalation as $x \to \infty$. Its non-linear nature differentiates it from linear functions.
• Example: $f(x) = 2^x$

Exponential Decay

• Characteristics: Rapid reduction as $x \to \infty$, approaching but never reaching the x-axis.
• Example: $f(x) = \left(\frac{1}{2}\right)^x$

Key Concepts and Techniques

Recognising Exponential Equations

• Exponential Equations: Involve equations where a constant base is exponentiated, usually in the form $a^x = b$.

• Visual Aids: Use diagrams and real-world contexts to differentiate between exponential and linear growth.

  

  • Exponential Growth Example: Typical in population growth models in biology.
  • Radioactive Decay Example: Commonly used in physics, particularly for half-life computations.

Solving Using Algebraic Methods

• Using Logarithms: Logarithms serve as effective instruments for solving exponential equations by converting them into linear forms.
  • Example: To solve $3^x = 27$, recast as $x = \log_3(27)$, then resolve using logarithmic principles.

• Interactive Example Steps: Prompt students to anticipate intermediate steps before unveiling solutions.
• Log Properties Guide:
  • Several properties assist in solutions, e.g., $\log(ab) = \log a + \log b$.

Real-World Applications

• Investigate practical applications emphasising real-world pertinence:

  • Population Growth Modelling: $N = 500 \times 1.5^t$, linking forecasts to demographic analysis.
  • Radioactive Decay: $N(t) = N_0 \times (1/2)^{t/T}$, pertinent in chemical dynamics.

• Narrative: Understanding these models facilitates insights into societal progressions.

Importance of Logarithms for Complex Solutions

• Real-Life Complexity: Logarithms simplify complex equations, such as those concerning pH levels.
• Detailed Transformation Example:
  • Step-by-step guidance utilising common ($\log$) and natural ($\ln$) logarithms.

Practice Problems

• Diverse Problem Set: Challenge students with both computational and conceptual questions, for example:
  • Addressing $2^{x+1} = 16$.
  • Solution: $2^{x+1} = 16$ $2^{x+1} = 2^4$ $x+1 = 4$ $x = 3$

Review and Challenge

• Address sophisticated problems necessitating strategic, multi-step reasoning.
• Common Pitfalls: Address errors such as incorrect logarithmic transformations.

Modelling with Exponential Functions

Introduction to Modelling with Exponential Functions

Modelling with Exponential Functions: Involves describing phenomena that expand or diminish rapidly over time.

• Relevance: Projections of everyday situations like population growth, or economic scenarios like increasing savings interest over time.

When to Use Exponential Models

• Rapid Growth Examples:

  • Adoption rates of emerging technologies.
  • Propagation of trends on social media.

• Natural Decay Examples:

  • Degradation of perishable items.
  • Ice reduction over time.

Examples of Exponential Modelling

• Population Dynamics:

  • Example: Doubling of weeds in a garden daily.
  • Model Setup:
    • Formula: $P(t) = P_0 e^{kt}$.
  • Worked Example:
    • Initial size $P_0 = 50$.
    • Calculate the number over subsequent days:
      • Day 1: $P(1) = 50 \times 2 = 100$.
      • Day 2: $P(2) = 100 \times 2 = 200$.

• Financial Investments:

  • Compound Interest:
  • Example: Interest in a savings account.
  • Formula: $A = P(1 + r/n)^{nt}$.

Challenges in Exponential Modelling

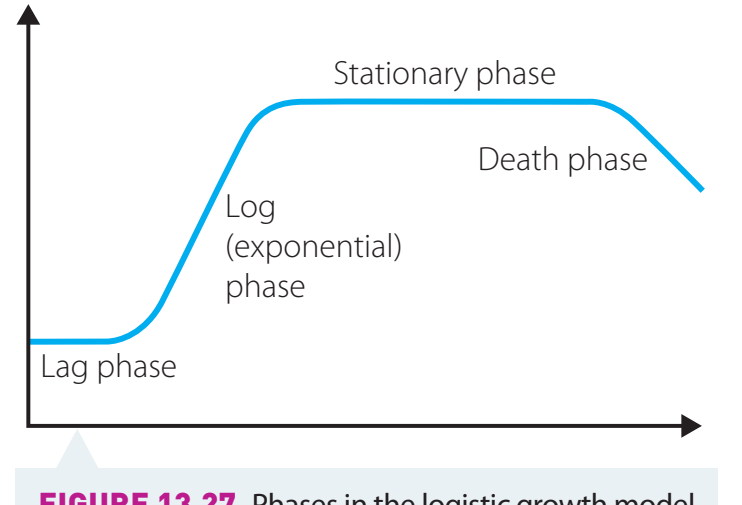
• Identifying Logistic Growth:

  • Filling a vessel with water—starts swiftly, then ceases when full.

• Bounded Growth Examples:

  • Ant colonies with limited resources—only a certain number of ants can thrive.

Application Problems

• Resource Limits:
  • Fish population in a pond, initially multiplying rapidly—slows as space becomes scarce.

Key Definition

Logarithms: The inverse of exponential operations.

• Equation Form: When $b^x = a$, it can be expressed as $\log_b(a) = x$.
• Understanding: $\log_b(a)$ indicates the power to which the base $b$ must be raised to attain $a$.

Properties and Laws of Logarithms

Utilise these principles for manipulating logarithmic expressions:

• Product Rule: $\log_b(MN) = \log_b(M) + \log_b(N)$
• Quotient Rule: $\log_b\left(\frac{M}{N}\right) = \log_b(M) - \log_b(N)$
• Power Rule: $\log_b(M^k) = k \times \log_b(M)$

Conversion Examples

Convert between exponential and logarithmic forms by:

1. Identify the base and resultant.
2. Apply the logarithmic format.

Examples:

• Convert $2^x = 8$ to: Result $x = \log_2(8) \Rightarrow x = 3$

Introduction to Practical Applications of Logarithmic Functions

Logarithms are indispensable for simplifying computations in real-life applications like acoustic intensity.

Worked Example: Calculating Sound Intensity Levels

Problem: Compute the decibel level derived from sound intensity.

• Solution Steps:
  • Step 1: Identify sound intensity ($I$) and reference intensity ($I_0$).
  • Step 2: Utilise the equation $dB = 10 \log_{10}\left(\frac{I}{I_0}\right)$.
  • Step 3: Resolve using the provided values.

Example:

• Given $I = 10^{-3}$ and $I_0 = 10^{-12}$:

  $dB = 10 \log_{10}\left(\frac{10^{-3}}{10^{-12}}\right) = 90 \text{ dB}$

Exam Strategies

• Ascertain whether the task pertains to growth or decay.
• Identify the given data.
• Formulate equations:
  • Example: $3^x = 27$, resolve by:
    • $\log(3^x) = \log(27)$
    • $x \cdot \log(3) = \log(27)$
    • $x = \frac{\log(27)}{\log(3)}$

Avoiding Common Pitfalls

Misinterpretations

• Switching Bases: Maintain uniformity to prevent inaccuracies.