Trig Functions and Optimisation

Trigonometric functions play a crucial role across diverse fields, including mathematics, physics, engineering, and navigation. Proficiency in their application significantly enhances problem-solving capabilities.

Introduction to Trigonometric Functions

Trigonometric Functions: Fundamental mathematical tools used to address real-world problems and delve into scientific applications.

Key Terms

• Periodicity: The regular intervals at which a function's values recur.
• Amplitude: The peak or maximal extent of a waveform.
• Frequency: The rate at which cycles occur within a specified time frame.

Key Characteristics of Trigonometric Functions

Periodicity

• Definition: Consistent intervals at which the function values repeat.
• Periods of Functions:
  • Sine: $2\pi$
  • Cosine: $2\pi$
  • Tangent: $\pi$

Amplitude

• Definition: The height or maximum deviation of a wave.
• Visual Impact: Larger amplitudes generate taller waves.
• Example: In the equation $y = 3\sin(x)$, the amplitude is 3.

Frequency

• Definition: The number of cycles within a given timeframe.
• Example: A wave completing 5 cycles in $2\pi$ exhibits a higher frequency than one completing a single cycle in the same interval.

Application of Trigonometric Functions

Trigonometric functions find applications in various disciplines.

Practical Applications

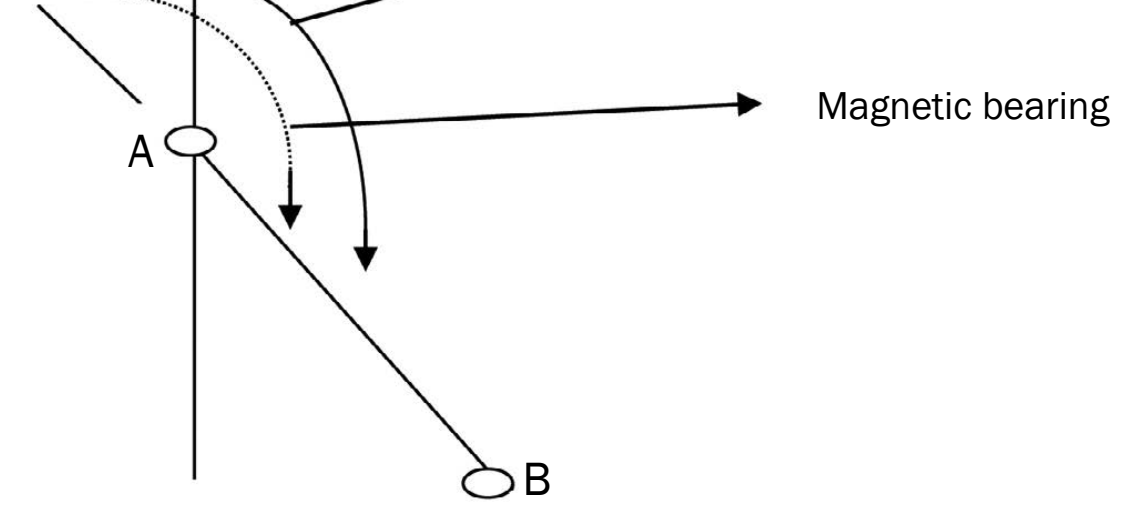
• Navigation: Utilises trigonometric equations for route planning and determining compass bearings.
  • Example: Compass bearings are measured in degrees from North.

• Physics: Examining oscillations and wave characteristics such as Simple Harmonic Motion (SHM): $y(t) = A \cos(\omega t + \phi)$.

• Engineering: Analyse AC circuits, resolve forces, and optimise structural designs.
  • Example: Use sine and cosine functions to resolve forces in truss analysis.

Strategies for Solving Contextual Problems

1. Identify Parameters: Determine known values and what needs to be found.
2. Method Selection: Select the appropriate trigonometric laws or techniques.
3. Validation: Verify solutions for correctness.

Optimisation Problems

Definition and Importance

• Optimisation problems: Focus on finding maximum or minimum values of functions under specific conditions.
• Relevance: Essential for enhancing system performance and resource efficiency.

Example Applications

• Sound Engineering: Improve audio quality by optimising wave properties.
• Projectile Motion: Maximise range and height through adjustments in angle and velocity.

Worked Example: Optimising Projectile Range

To find the angle that maximises a projectile's range:

1. The range equation is: $R = \frac{v_0^2\sin(2\theta)}{g}$
2. For maximum range, we need to maximise $\sin(2\theta)$
3. Since $\sin(2\theta)$ has a maximum value of 1 when $2\theta = 90°$
4. Therefore, $\theta = 45°$ gives the maximum range

This example shows how calculus and trigonometry work together to optimise physical systems.