Photo AI
Last Updated Sep 24, 2025
Trapezoidal Rule Integration Method Simplified Revision Notes for SSCE HSC Mathematics Advanced
Revision notes with simplified explanations to understand Trapezoidal Rule Integration Method quickly and effectively.
219+ students studying
Trapezoidal Rule Integration Method
Overview of Integral Calculus
Integral Calculus: A key branch of mathematics focused on integration, essential for determining areas under curves. It has applications across various fields, including mathematics, physics, electrical engineering, and economics.
Integral calculus complements differential calculus, offering a comprehensive analysis of functions.
Key Definitions
- Indefinite Integral: The antiderivative of a function, expressed as .
- Definite Integral: Computes the exact area under a curve between the limits and , represented as .
Introduction to the Trapezoidal Rule
Definition and Purpose
- Trapezoidal Rule: A numerical approach to approximate definite integrals utilising trapezoids.
- Essential in numerical integration when exact solutions are unavailable.
- Offers a practical method for estimating areas beneath curves.
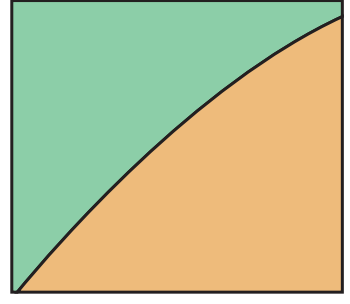
Definition: The Trapezoidal Rule approximates areas with trapezoids, simplifying integration when exact calculations are challenging.
Geometric Reasoning
- Why Trapezoids?
- Trapezoids align more closely with curves than rectangles, significantly minimising approximation errors.

Definition of Key Components
- Integral Limits: The start and end points ( and ).
- Endpoint Function Values: Evaluated at the boundaries of the interval, and .
- Intermediate Function Values: Evaluated at subinterval points, contributing to enhanced accuracy.
- Subintervals: Uniform divisions that improve precision.
Formula of the Trapezoidal Rule
The Trapezoidal Rule is expressed by the formula:
Worked Example and Derivation
Derivation Process
- Decompose the Interval: Divide the curve into equidistant trapezoids.
- Calculate Areas: Determine each area's size using the height and a sum-based base value.
- Develop Formula through geometric analysis.

Example Calculation
Example: Approximate using .
- Step 1: Compute the width: .
- Step 2: Evaluate the function values: , , .
- Step 3: Apply the formula:
Practice Problem with Solution
Problem: Calculate using .
Solution:
- Width:
- Function values:
- Apply the formula:
The exact value is 2, so our approximation is quite close.
Practical Applications
Land Measurement
- Vital in Civil Engineering for estimating areas of irregular plots.
- Example: With bases m and m, height m. Area = 1800 sq. m.
Volume Calculations
- Applied in Science and Engineering to estimate tank and container volumes.
- Example: Tank with bases m, m, height m. Volume = 250 m³.

Addressing Common Misconceptions
Misconception 1: Exact Results
- The Trapezoidal Rule provides approximate, not exact, results.
Misconception 2: Weights of Endpoint and Interior Values
- Endpoint values have less significance than interior ones.
By understanding the simplicity and limitations of the Trapezoidal Rule, students can effectively approximate integrals and apply these techniques across various disciplines.
500K+ Students Use These Powerful Tools to Master Trapezoidal Rule Integration Method For their SSCE Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
30 flashcards
Flashcards on Trapezoidal Rule Integration Method
Revise key concepts with interactive flashcards.
Try Mathematics Advanced Flashcards4 quizzes
Quizzes on Trapezoidal Rule Integration Method
Test your knowledge with fun and engaging quizzes.
Try Mathematics Advanced Quizzes29 questions
Exam questions on Trapezoidal Rule Integration Method
Boost your confidence with real exam questions.
Try Mathematics Advanced Questions27 exams created
Exam Builder on Trapezoidal Rule Integration Method
Create custom exams across topics for better practice!
Try Mathematics Advanced exam builder5 papers
Past Papers on Trapezoidal Rule Integration Method
Practice past papers to reinforce exam experience.
Try Mathematics Advanced Past PapersOther Revision Notes related to Trapezoidal Rule Integration Method you should explore
Discover More Revision Notes Related to Trapezoidal Rule Integration Method to Deepen Your Understanding and Improve Your Mastery
Load more notes