Areas Bounded by Y-Axis

Introduction

• Definite Integrals are the primary tool employed for calculating the area under a curve. This calculation is crucial for comprehending a variety of mathematical concepts and their applications, which include areas such as:

  • Physics: Assessing electricity consumption over time.
  • Economics: Evaluating economic growth and total income over certain periods.
  • Engineering: Designing objects and understanding structural loads over a specific area.

• Real-world Example: Consider calculating how much fuel a vehicle uses throughout a trip based on varying speeds. A definite integral allows for precise calculation of that fuel usage.

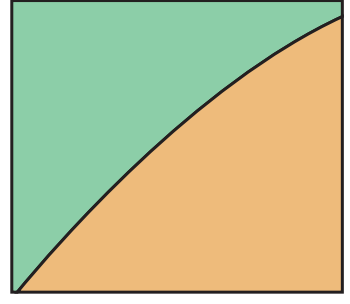
Concept Introduction

• Definition of Bounded Area: This term pertains to the region enclosed between two curves, evaluated along the y-axis. This method differs from evaluations along the x-axis due to the shift in variable focus.
• Significance of Initial Understanding: Grasping the concept of y-axis boundaries is essential for accurate calculations and serves as prerequisite foundational knowledge.

Diagrams

Fundamental Concepts

• When integrating with respect to the y-axis, we use vertical slices. This approach is advantageous for certain functions, simplifying the process when functions are naturally expressed as $x = f(y)$.

When to Use Vertical Slicing

• The function naturally resolves as $x = f(y)$.
• Simplification of the integration process concerning the x-axis.

Expressing Curves as $x = f(y)$

• To convert $y = g(x)$ to $x = f(y)$, solve for $x$.

Example:

• Start with $y = x^2 + 3$.
• Solve for $x$: $x = \sqrt{y - 3}$.

Additional Example:

• Given $y = 3x^2 + 2$, express this as $x = f(y)$.
• Begin by solving: $x^2 = \frac{y - 2}{3}$, thus $x = \sqrt{\frac{y - 2}{3}}$.

Setting Up Integrals

• Set up the integral using: $\int_{c}^{d} f(y)\,dy$

Setup Steps:

• Ensure the equation is $x = f(y)$.
• Identify limits: Lower Limit $(c)$, where the region starts; Upper Limit $(d)$, where the region concludes.

Step-by-Step Example:

• Convert $x = 2y$ and find the area between $y=1$ and $y=3$: $\int_{1}^{3} 2y \, dy$
• Compute: $[y^2]_{1}^{3} = 3^2 - 1^2 = 8$.

Common Student Misconceptions

• Variable inversion errors: Confusing $x$ and $y$.
• Misinterpreting the orientation and setup.

Practical Problem-Solving Strategies

• Analytical Approach: Break down complex problems into manageable sections for simpler, step-by-step evaluations.

• Visual Approach: Utilise graphs to transform abstract concepts into simpler visual forms for better understanding.

• Flowcharts: Map out each step of the problem-solving process visually through structured breakdowns.

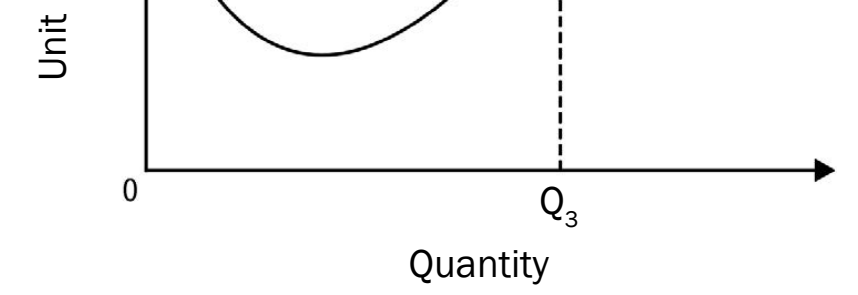
Worked Examples

Example 1: Linear Function

Linear functions help estimate trends like profit growth.

Steps:

• Identify: Establish limits from $x=0$ to $x=3$.
• Evaluate the integral: $\int_{0}^{3} (2x + 3) \, dx$
• First, integrate the expression: $(2x + 3)$ becomes $x^2 + 3x$ when integrated
• Then evaluate at the limits: $[x^2 + 3x]_{0}^{3} = (9 + 9) - (0 + 0) = 18$
• Therefore, the area is 18 square units

Example 2: Quadratic Function

Quadratic functions are used to model paths like projectiles in physics.

Steps:

• Define: Ensure limits accommodate the curve's behaviour.
• Solve: $\int_{1}^{4} (x^2 - 4x + 6) \, dx$
• Integrate each term: $\frac{x^3}{3} - 2x^2 + 6x$
• Evaluate at the limits: $[\frac{x^3}{3} - 2x^2 + 6x]_{1}^{4}$
• $(\frac{64}{3} - 32 + 24) - (\frac{1}{3} - 2 + 6) = \frac{64}{3} - 8 - \frac{1}{3} + 2 - 6 = \frac{63}{3} - 12 = 21 - 12 = 9$
• The area is 9 square units

Teaching and Error Correction Strategies

Instructional Techniques

• Structured, Step-by-Step Problem-Solving:

  • Begin with simple examples and gradually increase complexity.
  • Encourage students to describe their problem-solving process.
  • Worked Example with Context: For calculating the area bounded by $y = x^2$ from $y = 0$ to $y = 4$.
    • Step 1: Sketch the graph and determine why $y = x^2$ is chosen for integration.
    • Step 2: Set up the integral: $$\text{Area} = \int_0^4 (x=\sqrt{y}) \, dy$$
    • Step 3: Evaluate the integral: $$\text{Area} = \left[ \frac{2}{3}y^{3/2} \right]_0^4 = \frac{16}{3}$$

• Visual Learning Tools:

  • Utilise graphing calculators such as Desmos.
  • Employ colour-coding techniques to differentiate curves.

• Differentiated Instruction:

  • Design questions tailored to different skill levels.

Addressing Common Student Errors

Common Errors:

• Incorrect Integration Limits:

  • Misuse of intersection points.
  • Confusion regarding variable roles.

• Misidentification of Functions:

  • Confusing upper and lower boundaries.

• Misunderstanding Graphical Interpretations:

  • Incorrect visual representation of boundaries.

Strategies for Correction:

• Promote peer-teaching and collaborative learning.
• Provide guided resources for specific errors.
• Use targeted exercises and feedback from educators.
• Example Fixes: Compare student work with accurate models.

Utilising Visual and Interactive Tools

Tools:

• Interactive graphing tools (e.g., GeoGebra).
• Digital whiteboards for live problem-solving.
• Annotated diagrams for effective learning.

By implementing these strategies, visual aids, and interactive tools, students will be better equipped to apply integral calculus in practical scenarios, achieving both academic success and effective real-world problem-solving skills.