Area Formulae

Overview

Understanding the area of geometric shapes such as triangles, rectangles, circles, and composite shapes is fundamental for various academic and practical applications. These concepts are crucial in fields like architecture, engineering, and material estimation.

Accurate area calculations are essential for determining the amount of paint needed for a wall or the quantity of fabric required for a costume.

Key Characteristics of Geometric Shapes

Triangles

• Base: The horizontal side perpendicular to the height, vital in area calculations.
  infoNote

  Base: The foundational edge of a triangle, vital in area calculations.

• Height: Must be perpendicular to the base for accurate area calculation.
  chatImportant

  Height: A perpendicular line from the base to the opposite vertex, crucial in computations.

Area Formulae for Triangles

• Base-Height Method: $\frac{1}{2} \times \text{base} \times \text{height}$
  

• Heron's Formula for triangles with known sides:
  $\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
  where $s = \frac{a+b+c}{2}$

• Trigonometric Method for non-right-angled triangles:
  $\frac{1}{2} ab\sin(C)$
  

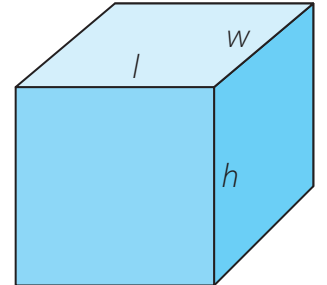
Rectangles

• Length & Width: The area is determined by multiplying length by width.
  chatImportant

  Area of a Rectangle:
  $\text{length} \times \text{width}$

  

Circles

• Radius: The central element in calculating a circle's area, measured from the centre to the edge.

  infoNote

  Radius vs Diameter: The radius is half of the diameter.

• π (pi): Approximately 3.14159, essential in circle calculations.

  chatImportant

  Area of a Circle:
  $\pi \times \text{radius}^2$

  

Composite Shapes

• Definition: Combinations of basic shapes to address practical problems.
• Example: Calculate the area of a rectangle topped with a semi-circle by treating each part separately.
  

Common Misconceptions

• Perimeter vs. Area: Perimeter measures the outer boundary; area measures the space within.
  infoNote

  Solution: Use visual aids to differentiate.

• Unit Misapplication: Ensure the use of consistent units to avoid calculation errors.
• Misunderstanding Heron's Formula: Ensure correct calculation of the semi-perimeter.

Teaching Strategies

• Visualisation: Use diagrams and models to teach concepts. Animated diagrams can enhance understanding for circles and sectors.
• Gradient Complexity: Start with basic problems and gradually increase difficulty.
• Mnemonic Devices: Assist in remembering key steps and formulae.

Examples and Practice Problems

Worked Examples

• Triangle

  • Given: Base = 6 cm, Height = 9 cm
  • Calculate: $\frac{1}{2} \times 6 \times 9 = 27 \text{ cm}^2$

• Rectangle

  • Given: Length = 12 cm, Width = 5 cm
  • Calculate: $12 \times 5 = 60 \text{ cm}^2$

• Circle

  • Given: Radius = 5 cm
  • Calculate: $\pi \times 5^2 \approx 78.54 \text{ cm}^2$

• Composite Shape

  • Rectangle with Semi-Circle Top
  • Calculate: $\text{Area Total} = \text{Area Rectangle} + \frac{1}{2} \pi r^2$
  • For example: If the rectangle is 10 cm × 6 cm and the semi-circle has radius 3 cm: $\text{Area Total} = (10 \times 6) + \frac{1}{2} \pi \times 3^2 = 60 + 14.14 = 74.14 \text{ cm}^2$

Practice Problems

• Triangle: Compute area for Base = 8 cm, Height = 5 cm.

  • Solution: $\frac{1}{2} \times 8 \times 5 = 20 \text{ cm}^2$

• Rectangle: Find the width if the area is 35 sq. cm. and length is 7 cm.

  • Solution: $\text{Width} = \frac{\text{Area}}{\text{Length}} = \frac{35}{7} = 5 \text{ cm}$

• Circle: Determine the area with a diameter of 12 cm.

  • Solution: $\text{Radius} = \frac{\text{Diameter}}{2} = 6 \text{ cm}$, $\text{Area} = \pi \times 6^2 \approx 113.1 \text{ cm}^2$

• Composite: Calculate the area of a square with side 8 cm that has a semicircle of radius 4 cm attached to one side.

  • Solution: $\text{Square area} = 8^2 = 64 \text{ cm}^2$, $\text{Semicircle area} = \frac{1}{2} \pi \times 4^2 = 25.13 \text{ cm}^2$
  • $\text{Total area} = 64 + 25.13 = 89.13 \text{ cm}^2$

Advanced Concepts

Similarity and Scale Factor

• Similarity: Shapes with identical shapes but varying sizes.
• Scale Factor: The ratio affecting area based on dimension changes.
  infoNote

  Example: Doubling the side length increases the area fourfold.

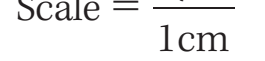
Visual Tools

• Use graph paper and software like GeoGebra for precise diagrams. Ensure accurate measurements.
  

Exam Tips and Checklist

• Key Strategies:
  • Regularly engage with different methods.
  • Use visual tools for clarity.
  • Apply to real-world scenarios for contextual understanding.
• Checklist for Exams:
  • Ensure diagram precision.
  • Confirm understanding through practical uses.
  • Discuss and correct errors in peer groups.

Incorporating these techniques and strategies will enhance students' skills in area calculations, adequately preparing them for exams and real-world problem-solving scenarios.