Photo AI
Last Updated Sep 26, 2025
Exponential Functions Explained Simplified Revision Notes for SSCE HSC Mathematics Advanced
Revision notes with simplified explanations to understand Exponential Functions Explained quickly and effectively.
359+ students studying
Exponential Functions Explained
Exponential functions are essential components in calculus, modelling natural growth and decay. This note delineates important concepts, properties, and applications of exponential functions and their inverses, with a specific emphasis on Euler's number, .
Key Terms: Definitions
- Euler's Number : Approximately 2.71828. It serves as the base for natural logarithms and is pivotal for continuous growth models in mathematics.
- Exponential Function: Represented as , where is a constant.
- Natural Logarithms: These are the inverses of exponential functions, denoted as .
Understanding Differentiation of
- Differentiation Formula:
- The Derivative of is : .
- Uniqueness: This property indicates that the function grows at a rate proportional to its value, a unique aspect in calculus.
Derivation Steps:
- Begin with the limit definition:
- Factor out :
- Constant Explanation: The limit is fundamental for validating properties of exponential growth.
Euler's number is crucial for modelling continuous growth in nature and exponential functions.
Euler's Number,
- Definition and Limit Definition:
- Euler's Number (e):
Historical Context:
- Discovery:
- Initially identified by Jacob Bernoulli through his study of compound interest.
- Development:
- Leonhard Euler expanded its application in calculus with rigorous proofs.
Significance in Exponential Functions
- Derivative Property:
- Uniqueness:
- The distinguishing feature of is that its derivative is , highlighting a constant rate of steep ascension.
- Uniqueness:
- Fundamental Role of Logarithms:
- Being the base of natural logarithms makes it indispensable for resolving growth and decay equations.
Natural logarithms employ for modelling continuous processes.
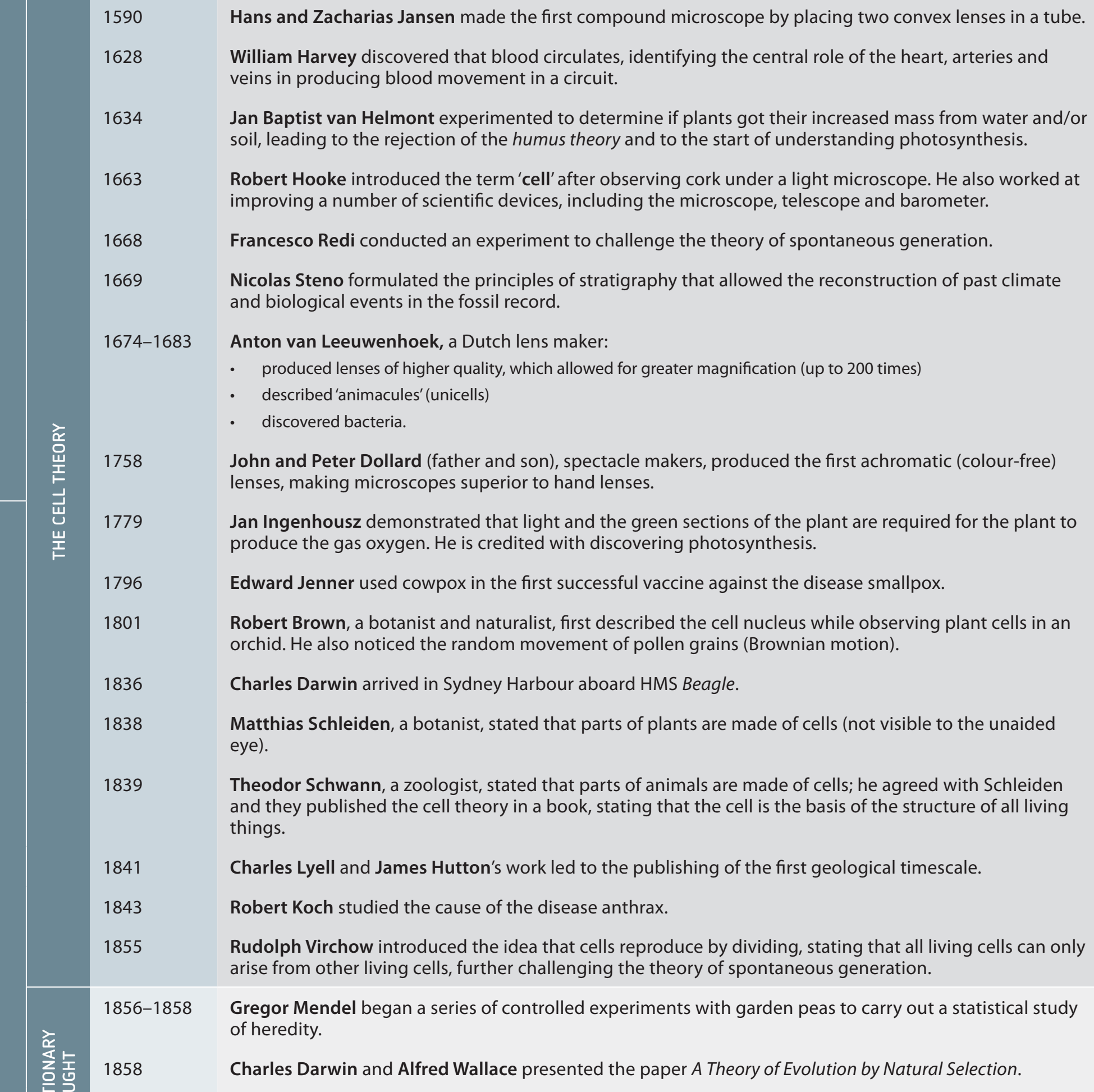
Graphical Behaviour of
Graph Characteristics:
- Exponential Growth:
- The graph displays rapid ascent as increases.
- Constant Slope:
- The graph maintains consistent growth, with tangent line slopes equaling the function values at any point.
- Asymptotic Behaviour:
- Approaches the x-axis but never intersects it.
Applications and Worked Examples
Worked Examples
- Example 1: Differentiate .
- Solution: .
- Example 2: Differentiate .
- Let's break this down step by step:
- Apply the chain rule:
- Differentiate the inner function:
- Therefore:
- Let's break this down step by step:
Continuous Growth Models
- Real-life Applications:
- Commonly used in calculating Compound Interest and modelling Population Growth.
Common Errors
- Mistakes with Exponents:
- Avoid altering the base or mishandling exponents when performing differentiation.
Inverse Relationship: Exponential and Logarithmic Functions
Definitions and Properties
- Inverse Functions:
- The operations of and effectively neutralise each other.
- Key Properties:
- Domain for :
- Domain for :
Graphical Representation
- Reflection Across :
- The inverse relationship is evident through their mirrored graphs.
Problem Solving
- Algebraic and Graphical Applications:
- Confirm transformations by verifying reflections.
Exam Tips
- Remember to thoroughly verify the domains of exponential and logarithmic functions to prevent errors.
- Employ graphing technology for visualising problems, ensuring accuracy in solutions.
500K+ Students Use These Powerful Tools to Master Exponential Functions Explained For their SSCE Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Exponential Functions Explained
Revise key concepts with interactive flashcards.
Try Mathematics Advanced Flashcards2 quizzes
Quizzes on Exponential Functions Explained
Test your knowledge with fun and engaging quizzes.
Try Mathematics Advanced Quizzes29 questions
Exam questions on Exponential Functions Explained
Boost your confidence with real exam questions.
Try Mathematics Advanced Questions27 exams created
Exam Builder on Exponential Functions Explained
Create custom exams across topics for better practice!
Try Mathematics Advanced exam builder5 papers
Past Papers on Exponential Functions Explained
Practice past papers to reinforce exam experience.
Try Mathematics Advanced Past PapersOther Revision Notes related to Exponential Functions Explained you should explore
Discover More Revision Notes Related to Exponential Functions Explained to Deepen Your Understanding and Improve Your Mastery
Load more notes