Derivative First Principles

Introduction

• Limit: A limit in calculus signifies the value a function approaches as the input draws near a specific point. Limits are vital for deriving derivatives, which measure instantaneous rates of change. For example, imagine a car slowing gradually to a stop at traffic lights—its speed reducing to zero akin to a function approaching a limit.

• Derivative: The gradient of the tangent line to the curve of a function at a specific point, serving as a bridge between algebra and geometry.

The Derivative Quotient

• Formal Definition: $\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$

• Significance: Used to predict trends in graphs, model biological processes, and measure athletic acceleration.

• Misconceptions about Limits:

  • Limits are dynamic entities, not static.
  • Example: Evaluate $\lim_{x \to 2} \frac{x^2 - 4}{x - 2}$, even though it is undefined at $x=2$.

Finding Derivatives from First Principles

• Utilise the limit definition of a derivative: $\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$ to find the derivative of function: $f(x) = x^2$.

Step-by-Step Derivation Example

• Initial Setup:

  • Expression: $f(x+h) = (x+h)^2$.

• Expand & Simplify:

  • Expand: $(x+h)^2 = x^2 + 2xh + h^2$.
  • Simplify: $\frac{(x^2 + 2xh + h^2) - x^2}{h} = \frac{2xh + h^2}{h} = 2x + h$.

• Apply the Limit:

  • Result: $f'(x) = \lim_{h \to 0} (2x + h) = 2x$.

Numerical and Graphical Illustrations

Numerical

• Approach: Numerical calculations of $\frac{f(x+h)-f(x)}{h}$ become more accurate as $h$ decreases, providing improved approximations.

  

Graphical

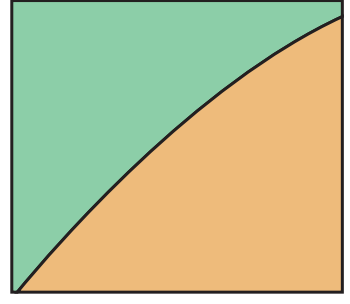
• Visualise: Secant lines gradually converge to tangent lines as $h \to 0$.

  

Numerical Estimation

• Numerical Methods: Provide approximations for derivatives when analytical solutions are not feasible.
• Finite Difference Methods:
  • Forward: $f'(x) \approx \frac{f(x+h) - f(x)}{h}$.
  • Backward: $f'(x) \approx \frac{f(x) - f(x-h)}{h}$.
  • Central: $f'(x) \approx \frac{f(x+h) - f(x-h)}{2h}$.
  

Error Analysis

• Types:

  • Truncation errors arise from approximations.
  • Round-off errors result from the finite precision of computing.
  • Mitigation: Careful selection of interval sizes and strategic error reduction methods.

  

Practice Problems with Solutions

Problem 1: Derive $f(x) = x^3$ from first principles.
Solution:

1. Begin with the definition: $f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$
2. Substitute $f(x) = x^3$: $f'(x) = \lim_{h \to 0} \frac{(x+h)^3-x^3}{h}$
3. Expand $(x+h)^3 = x^3 + 3x^2h + 3xh^2 + h^3$
4. Simplify: $f'(x) = \lim_{h \to 0} \frac{x^3 + 3x^2h + 3xh^2 + h^3 - x^3}{h} = \lim_{h \to 0} \frac{3x^2h + 3xh^2 + h^3}{h} = \lim_{h \to 0} (3x^2 + 3xh + h^2)$
5. Apply the limit: $f'(x) = 3x^2$

Problem 2: Use the limit definition to derive $f(x) = \frac{1}{x}$. Solution:

1. Begin with the definition: $f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$
2. Substitute $f(x) = \frac{1}{x}$: $f'(x) = \lim_{h \to 0} \frac{\frac{1}{x+h}-\frac{1}{x}}{h}$
3. Find a common denominator: $f'(x) = \lim_{h \to 0} \frac{\frac{x-(x+h)}{x(x+h)}}{h} = \lim_{h \to 0} \frac{\frac{-h}{x(x+h)}}{h}$
4. Simplify: $f'(x) = \lim_{h \to 0} \frac{-1}{x(x+h)} = \frac{-1}{x^2}$
5. Therefore, $f'(x) = -\frac{1}{x^2}$