Photo AI
Last Updated Sep 24, 2025
Locus in Mathematics Simplified Revision Notes for SSCE HSC Mathematics Advanced
Revision notes with simplified explanations to understand Locus in Mathematics quickly and effectively.
429+ students studying
Locus in Mathematics
Introduction
Loci: A crucial concept in understanding the distribution of shapes and curves in space, loci describe sets of points that fulfil specific mathematical conditions. They are essential for both theoretical geometry and practical applications, including satellite dish design and calculation of planetary orbits.
Coordinate Geometry Applications:
- Utilised in project designs to ensure precision.
- Improves mapping accuracy in navigation systems.
Definition and Basic Principles
Locus: A set of points meeting defined geometric conditions forms the basis of many geometric principles. These are essential for tackling a range of geometric problems.
Locus: A set of points that satisfy specific geometric conditions.
Visualising the Concept of Locus
- Circle: Represents a locus of points equidistant from a central point.
- Line: Represents a locus equidistant from two parallel lines.

Key Geometric Shapes and Their Properties
- Circles:
- Definition: Locus of points equidistant from a central point.
- Equation: , where is the centre and is the radius.
- Features:
- Radius: Determines the size of the circle.
- Diameter: Always double the radius.
Remember, the diameter is always twice the radius. It cannot be the other way around!

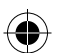
- Parabolas:
- Definition: The locus is equidistant from a fixed point (focus) and a line (directrix).
- Key Equations: or .
- Ellipses & Hyperbolas:
- Ellipses Definition: Locus with a constant sum of distances from two fixed points (foci).

- Hyperbolas Definition: Locus where the difference in distances to two fixed points (foci) remains constant.
Equation of a Locus from Geometric Conditions
Understanding Loci Equations
Loci equations are commonly encountered in exams. They describe the path of points meeting specified conditions, such as being equidistant from others.
- Identify the geometric condition:
- Recognise essential characteristics, such as equidistant points.
- Translate to a mathematical expression:
- Implement the distance formula.
- Simplify and resolve:
- Equate, simplify, and solve the expression.
Key Terms: Locus: A set of points that meets specific conditions.
Detailed Examples
1. Equidistant from Two Points
- Forms the perpendicular bisector of the line segment joining two points.
Worked Example: Let's find the locus of points equidistant from points A(2,3) and B(6,7).
Step 1: For any point P(x,y) on the locus, PA = PB. Step 2: Using the distance formula:
Step 3: Square both sides to eliminate the square roots:
Step 4: Expand:
Step 5: Simplify:
The locus is the straight line with equation x + y = 9, which is the perpendicular bisector of the line segment AB.
2. Constant Distance from a Line
- Identifies lines parallel to the given line.
3. Fixed Distance from a Point
- Derives the equation of a circle.
Ensure accuracy in every step, especially during simplifications where errors might lead astray.
Techniques for Deriving Loci Equations
- Break down each condition using visual aids for clarity.
- Avoid common errors, such as failing to square terms and incorrect algebra.
Principles of Coordinate Geometry for Loci
Distance Formula
- Formula:
Grid and Plot Points
- Steps to Plotting:
- Identify points and plot them accurately on the grid.
- Depict loci using the plotted points.
Common pitfall: Watch out for coordinate signs. Double-check to ensure correctness!
Strategies for Approaching Complex Locus Problems
- Read Carefully: Comprehend each component and constraint thoroughly.
- Visualise: Utilise diagrams to aid understanding and resolve difficulties.
- Step-by-step Analysis: Deconstruct problems, solve systematically, and integrate solutions.
500K+ Students Use These Powerful Tools to Master Locus in Mathematics For their SSCE Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Locus in Mathematics
Revise key concepts with interactive flashcards.
Try Mathematics Advanced Flashcards5 quizzes
Quizzes on Locus in Mathematics
Test your knowledge with fun and engaging quizzes.
Try Mathematics Advanced Quizzes29 questions
Exam questions on Locus in Mathematics
Boost your confidence with real exam questions.
Try Mathematics Advanced Questions27 exams created
Exam Builder on Locus in Mathematics
Create custom exams across topics for better practice!
Try Mathematics Advanced exam builder5 papers
Past Papers on Locus in Mathematics
Practice past papers to reinforce exam experience.
Try Mathematics Advanced Past PapersOther Revision Notes related to Locus in Mathematics you should explore
Discover More Revision Notes Related to Locus in Mathematics to Deepen Your Understanding and Improve Your Mastery
Load more notes