Linear Equations with Fractions

Introduction

Linear equations play a significant role in mathematics due to their capacity to systematically model and resolve diverse problems. Comprehending them is beneficial in real-world situations such as budgeting and crafting recipes. For instance: "How might you divide the expenses when sharing a meal?" This scenario calls for applying mathematical skills.

Definition and Importance of Linear Equations

• Linear Equation: An algebraic statement where the variable quantities form a straight line when graphed.
• Importance: They are crucial for solving a variety of mathematical problems and have extensive applications, such as calculating loan amounts or determining material quantities.

The Role of Fractions

Fractions add complexity to solving linear equations:

• Fractions necessitate extra steps for simplification.
• Fractional coefficients introduce intricate calculations.

Introduction to Fractions

Definition

• Fractions represent parts of a whole using two numbers, vital in solving equations, particularly linear ones.
• Numerator: The upper number, indicating the number of parts taken.
• Denominator: The lower number, showing the total number of parts.

Types of Fractions

• Proper Fractions: Numerator < Denominator
• Improper Fractions: Numerator ≥ Denominator
• Mixed Numbers: Combination of a whole number and a proper fraction

Clearing Fractions

Key Definition

• Least Common Denominator (LCD): The smallest multiple shared by all denominators. Crucial when solving equations.

Step-by-Step Process

1. Find the LCD:
   • Identify the least common multiple of all denominators.
2. Multiply Each Term by the LCD:
   • Simplify by applying this number to every term.

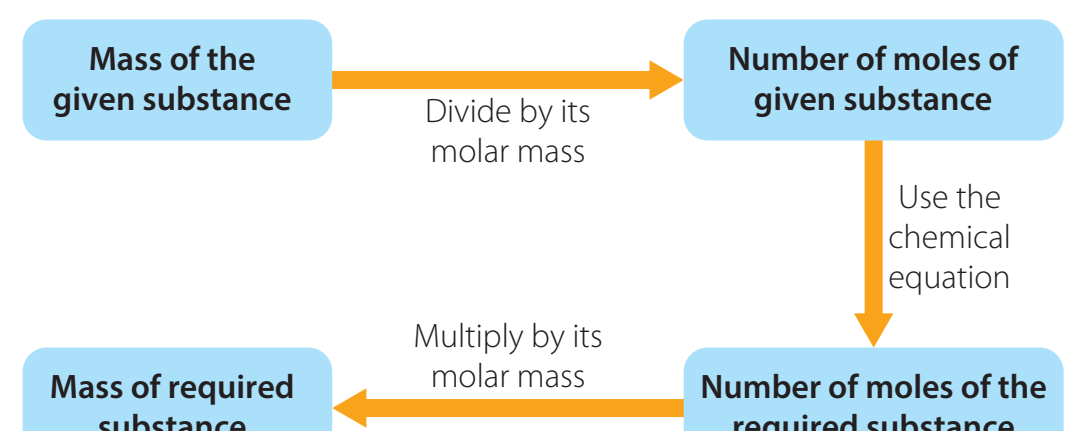
Solving Linear Equations

Techniques for Solving Linear Equations

• Addition and Subtraction: Isolate the variable. For instance:

  • $x + 5 = 8$
  • Subtract 5 from both sides: $x = 3$

• Multiplication and Division: Adjust coefficients where necessary.

  • Example: $2x = 10$: Divide by 2, $x = 5$

Handling Fractions

• Fractional Coefficients:
  • Eliminate fractions by multiplying; for example:
    • Solve $\frac{1}{2}x = 4$ by multiplying both sides by 2, leading to $x = 8$

Verification of Solutions

Importance

Verification ensures accuracy in mathematical calculations.

Method of Verification: Substitution

• Example Equation: $2x + 3 = 7$
• Solution: $x = 2$
• Verification Step: Substitute the solution back: $2(2) + 3 = 7$, confirming the solution is correct.

Common Mistakes in Fractions

• Sign Errors:
  • Incorrect manipulation can result in errors.
• Fractions Misuse:
  • Identify errors in multiplying/dividing fractions.

Practical Examples and Solutions

Example 1: Simple Equation

• Solve $\frac{1}{2}x + \frac{1}{3} = x - \frac{4}{3}$
• Multiply every term by 6 (the LCD) to get $3x + 2 = 6x - 8$.
• Simplify to $3x + 2 + 8 = 6x$, giving $10 = 3x$, yielding $x = \frac{10}{3}$.

Common Misinterpretations

• Incorrect Fractions: Using the correct common denominators ensures accuracy.

Practice Exercises

1. Solve $\frac{3}{4}x - \frac{1}{2} = \frac{2}{3}$

   • Solution: First, find the LCD which is 12.
   • Multiply all terms by 12: $9x - 6 = 8$
   • Add 6 to both sides: $9x = 14$
   • Divide by 9: $x = \frac{14}{9}$

2. Find $x$: $\frac{5}{6}x + 3 = \frac{1}{2}x + \frac{1}{3}$

   • Solution: LCD is 6.
   • Multiply all terms by 6: $5x + 18 = 3x + 2$
   • Subtract 3x from both sides: $2x + 18 = 2$
   • Subtract 18 from both sides: $2x = -16$
   • Divide by 2: $x = -8$

---

Being adept at these concepts prepares you for advanced mathematics!