Midpoint and Distance Formulas

Overview

• Objective: Enhance strategies for effective teaching and assessment of understanding midpoint and distance formulas.
• Core Focus: Stress on improving student comprehension through comprehensive instruction and assessment techniques.

Introduction to the Number Plane

The number plane is a fundamental concept in mathematics used for plotting points and visually demonstrating relationships between numbers. It illustrates how numbers interact within a two-dimensional space.

Cartesian Coordinate System

The number plane employs the Cartesian coordinate system, which comprises two perpendicular axes intersecting at the origin (0,0). The position of each point on the plane is determined using these axes.

Components of the Number Plane

• Axes:

  • X-axis: Represents the horizontal line.
  • Y-axis: Denotes the vertical line.
  • Meeting point at the origin: (0,0).

• Quadrants:

  • The plane is divided into four sections known as quadrants:
    • Quadrant I: Positive x and y.
    • Quadrant II: Negative x, positive y.
    • Quadrant III: Negative x and y.
    • Quadrant IV: Positive x, negative y.
  chatImportant

  Understanding axes and quadrants is essential for locating points on the number plane.

• Plotting Points:

  • Coordinates: Points are denoted as (x, y).
  • Guideline: First move horizontally for x, then vertically for y.
  • Examples: To plot (3, -2), move 3 units to the right and 2 units down from the origin.

  

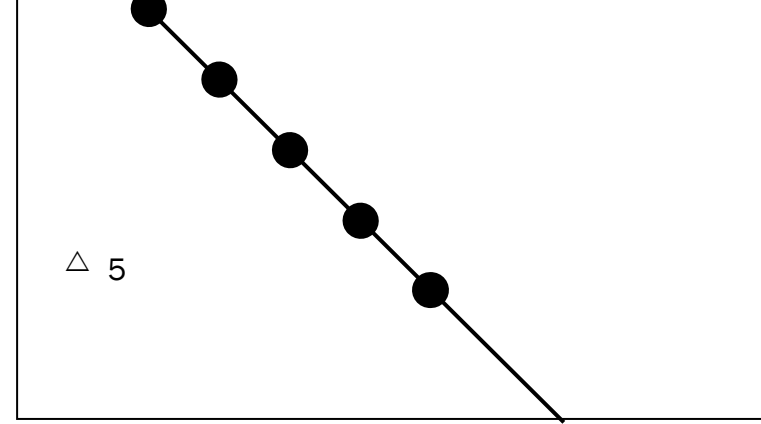
Introduction to the Distance Formula

Distance Formula: A mathematical approach to calculate the distance between two points on a coordinate plane.

• Importance: Crucial in geometry, navigation, and urban planning.
• Equation: $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.

Understanding the Pythagorean Theorem

This theorem forms the basis of the distance formula:

• Equation: $a^2 + b^2 = c^2$.
• Elements:
  • Hypotenuse: The longest side of a right triangle.
  • Legs: The two shorter sides.

Worked Examples

1. Compute the distance between $(0, 0)$ and $(3, 4)$:

   • Solution: $\sqrt{3^2 + 4^2} = 5$.

2. Determine the distance between $(2, 3)$ and $(5, 7)$:

   • Solution: $\sqrt{(5-2)^2 + (7-3)^2} = 5$.

Definition and Importance of Midpoint

• Midpoint: A point that divides a line segment into two equal segments.

Midpoint Calculation Formula

The formula to compute the midpoint is: $M = \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$

Calculating Midpoints: Worked Examples

1. Calculate the midpoint of the line segment with endpoints $(2, -1)$ and $(10, 3)$:

   • Solution Steps:
     • Compute x-average: $(2 + 10)/2 = 6$.
     • Compute y-average: $(-1 + 3)/2 = 1$.
     • Midpoint: $(6, 1)$.

2. Calculate the midpoint of the line segment with endpoints $(-4, 7)$ and $(6, -3)$:

   • Solution Steps:
     • Compute x-average: $(-4 + 6)/2 = 1$.
     • Compute y-average: $(7 + (-3))/2 = 2$.
     • Midpoint: $(1, 2)$.

Applications in Real-world Scenarios

Mapwork

• Steps to Determine Distances:

  • Identify coordinates: Find two points on a map.
  • Apply formula: Use the distance formula for calculation.
  infoNote

  Visualise these steps using the following flowchart to aid comprehension:

Example Exercise

Calculate the distance between two cities using their coordinates on a map.

• Cities' Coordinates:

  • City A: $(2, 3)$
  • City B: $(10, 11)$

• Calculation: $\text{Distance} = \sqrt{(10 - 2)^2 + (11 - 3)^2} = \sqrt{8^2 + 8^2} = \sqrt{128} \approx 11.31$

  Solution: The distance between the cities is approximately 11.31 units.

Ensure to convert the map measurement to a real-world distance by applying the map's scale.

Architectural Design

• Determine the Midpoint:
  • Find the midpoint for a proposed building site with corners $(1,3)$ and $(9,11)$.
  • Solution:
    • x-coordinate: $(1+9)/2 = 5$
    • y-coordinate: $(3+11)/2 = 7$
    • Midpoint = $(5, 7)$

Introduction to Common Misconceptions and Errors

Conceptual Clarifications:

• Distance evaluates the separation between two points using the formula $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
• Midpoint identifies the central point using $M = \left( \frac{(x_1 + x_2)}{2}, \frac{(y_1 + y_2)}{2} \right)$.

Identifying Frequent Errors

Confusing Distance and Midpoint Formulas

• Distinct Functions and Correct Applications:
  • Distance formula computes how far two points are apart.
  • Midpoint formula identifies the central point.

Sign Errors in Calculations

• Checklist for Ensuring Accuracy:
  • Thoroughly verify each calculated sign.

Strategies to Overcome Misconceptions

• Problem-Solving Techniques:
  • Engage with visual aids and examples for enhanced clarity.

Techniques for Distinguishing Between Formulas

Identifying Clues:

• When to apply each formula:
• Use square and square root operations for distance.
• Use averaging for midpoint.

Teaching Strategies

• Visual Aids:

  • Utilise visual tools to depict coordinates.
  infoNote

  Incorporating visual aids facilitates interactive understanding.

Recommendations

• Real-World Contexts:

  • Foster engagement by linking mathematical concepts to real-life situations.
  chatImportant

  Incorporating real-world scenarios significantly enhances engagement and retention.