The Definite Integral: Core Concepts

Introduction

Integral calculus is fundamental for resolving questions related to the area under curves and volumes.

• Computing these areas and solving problems associated with volumes requires integral calculus.
• The development of integral calculus by Isaac Newton and Gottfried Leibniz has profoundly influenced modern problem-solving techniques.

Key Terms and Definitions

• Anti-Derivative: The original function used to find families of integrals.

  • Essential for reversing differentiation and ensuring solution accuracy.
  infoNote

  Anti-Derivative: Key for determining families of integrals and validating solutions.

• Integrand: The function being integrated; indispensable for solving problems.

  • Example: In $\int x^2 \, dx$, the integrand is $x^2$.
  infoNote

  Integrand: Represents the function being integrated, vital for tackling problems.

• Upper/Lower Limits: Define the range for definite integrals, essential for addressing bounded problems.

  infoNote

  Upper/Lower Limits: Set the boundaries for definite integrals, crucial for solving problems.

The Dual Nature of Calculus

• Inverse Relationship: Integration reconstructs what differentiation deconstructs, aiding in solution verification.

  • Mathematical Example:

  $F(x) = \int x^2 \, dx = \frac{x^3}{3} + C$

  Differentiating $\frac{x^3}{3} + C$ restores $x^2$.

Definition and Contrast with Indefinite Integrals

• Definite Integral: Used to compute the exact area under a curve between specified boundaries, providing a precise numerical value.
  • Produces an exact numerical outcome, unlike indefinite integrals, which yield a family of functions as anti-derivatives.

Mathematical Notation of the Definite Integral

• Notation Components:
  • $a$ - Lower limit of integration.
  • $b$ - Upper limit of integration.
  • $f(x)$ - Function being integrated (integrand).
  • $dx$ - Infinitesimal change in x.

Properties of Definite Integrals

• Key Properties:
  • Linearity:
    • $\int_a^b [cf(x) + g(x)]\, dx = c \int_a^b f(x)\, dx + \int_a^b g(x)\, dx$
  • Additivity:
    • $\int_a^c f(x)\, dx = \int_a^b f(x)\, dx + \int_b^c f(x)\, dx$
  • Effect of Limits: Swapping limits changes the sign of the integral.

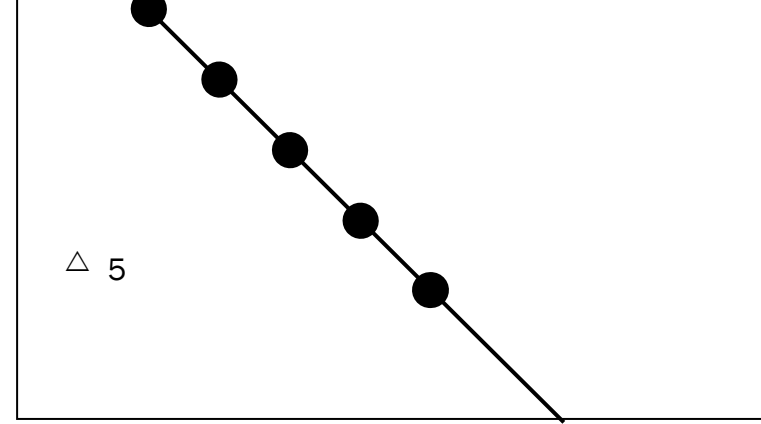
Geometric Interpretation of Definite Integrals

• Area Under a Curve: Represents the total area between the curve and the x-axis. Positive areas lie above the axis, while negative areas are below.

Example Calculations

• Example 1:
  • Problem: Calculate the definite integral of $f(x) = 2x + 3$ from $x=1$ to $x=4$.
  • Solution:
    • Find the antiderivative: $F(x) = x^2 + 3x + C$
    • Evaluate at the limits: $F(4) - F(1)$
    • $F(4) = 16 + 12 = 28$
    • $F(1) = 1 + 3 = 4$
    • Therefore: $28 - 4 = 24$

• Example 2:
  • Trigonometric Problem: Evaluate $\int_0^\pi \sin(x)\, dx$.
  • Solution:
    • The antiderivative of $\sin(x)$ is $-\cos(x) + C$
    • Evaluate at the limits: $[-\cos(\pi) + C] - [-\cos(0) + C]$
    • $[-\cos(\pi)] - [-\cos(0)] = -(-1) - (-1) = 1 + 1 = 2$

The Fundamental Theorem of Calculus

Introduction

The Fundamental Theorem of Calculus connects differentiation with integration, revolutionising problem-solving across multiple fields.

Theorem Breakdown

• Part 1:

  $\int_a^b f(x)\, dx = F(b) - F(a)$

• Part 2:

  $\frac{d}{dx} \left( \int_a^x f(t)\, dt \right) = f(x)$

Applications

Applications include:

• Physics: Integrate forces over a distance; derivatives provide instantaneous speeds or accelerations.

• Economics: Facilitate budgeting and projections by integrating consumption over time.

Misconceptions and Tips

• Check Integral Bounds: Ensure bounds are properly aligned with variables and limits.
• Practice Deliberately: Use varying bounds creatively to increase accuracy.

Example: Using Part 2

• Calculate: $\int_0^x \cos(t)\, dt$

• Step-by-step:

  • Function: $f(t) = \cos(t)$
  • Ensure Continuity: Confirm $f(t)$ is continuous over the defined interval.
  • Apply Part 2: Differentiating $\int_0^x \cos(t)\, dt$ results in $\frac{d}{dx} = \cos(x)$.

Visual Example:

Summary

By linking integration and differentiation, integral calculus forms the foundation of advanced calculus studies. Achieving mastery provides a robust framework for further studies.

Example Problems

Polynomial Functions

• Problem: Determine $\int (4x^3 + 6x^2) \, dx$
• Solution:
  1. Integrate each term separately:
     • $\int 4x^3 \, dx = 4 \cdot \frac{x^4}{4} = x^4$
     • $\int 6x^2 \, dx = 6 \cdot \frac{x^3}{3} = 2x^3$
  2. Combine results: $x^4 + 2x^3 + C$

Trigonometric Functions

• Problem: Find $\int \sin(2x) \, dx$
• Solution:
  1. Use substitution: let $u = 2x$, then $du = 2\,dx$ or $dx = \frac{du}{2}$
  2. Rewrite: $\int \sin(2x) \, dx = \int \sin(u) \cdot \frac{du}{2} = \frac{1}{2} \int \sin(u) \, du$
  3. Integrate: $\frac{1}{2} \cdot (-\cos(u)) + C = -\frac{1}{2}\cos(2x) + C$

Exponential Functions

• Problem: Compute $\int e^{3x} \, dx$
• Solution:
  1. For exponentials of form $e^{ax}$, the integral is $\frac{1}{a}e^{ax} + C$
  2. Apply with $a = 3$: $\frac{1}{3}e^{3x} + C$

Rational Functions

• Problem: Evaluate $\int \frac{1}{x^2 - x} \, dx$
• Solution:
  1. Decompose using partial fractions: $\frac{1}{x(x-1)} = \frac{A}{x} + \frac{B}{x-1}$
  2. Find common denominator: $\frac{A(x-1) + Bx}{x(x-1)} = \frac{1}{x(x-1)}$
  3. Comparing numerators: $A(x-1) + Bx = 1$
  4. Setting up a system of equations:
     • When $x = 0$: $-A = 1$, so $A = -1$
     • When $x = 1$: $B = 1$
  5. Therefore: $\frac{1}{x^2 - x} = \frac{-1}{x} + \frac{1}{x-1}$
  6. Integrate: $\int \frac{1}{x^2 - x} \, dx = -\ln|x| + \ln|x-1| + C = \ln|\frac{x-1}{x}| + C$

Methods

• Substitution Method: Substitution employs single variables for streamlined integration.

• Integration by Parts: Applicable to products of functions.

• Partial Fractions: Facilitates the decomposition of rational expressions.

Enhancing Conceptual Understanding

• Overcome Challenges:

  • Misunderstandings may arise from incorrect limit usage.
  • Utilise graphing utilities for spatial insight.

• Formulate Strong Foundations:

  • Employ diagrams for a geometric perspective.
  • Segment complex problems into manageable parts.

• Engagement and Relevance:

  • Highlight real-world applications in contexts such as physics and economics.
  • Promote discussions for varied problem-solving methodologies.

Consistent practice, interactive learning, and conceptual clarity are pivotal for mastering definite integrals and primitive functions.