Parabola as Locus

Introduction to the Locus Concept

Locus: The collection of all points that meet a specified condition in a plane. What shape emerges when each point adheres to a certain rule?

Everyday Examples and Visualisation

• Garden Sprinkler: As the sprinkler turns, the water droplets form a circle, illustrating a simple locus.
  • "This vividly shows how loci manifest in everyday settings."
• Widening Ripple: When a stone is thrown into water, ripples expand in circles where it lands. Each circle forms a locus.
  • Geometric basis reinforces understanding: "Ripples create concentric circles based on their distance from the point of impact."
• Compass Drawing: Drawing with a compass results in a circle by remaining at a consistent distance from the centre point.

Visualisation through Diagrams

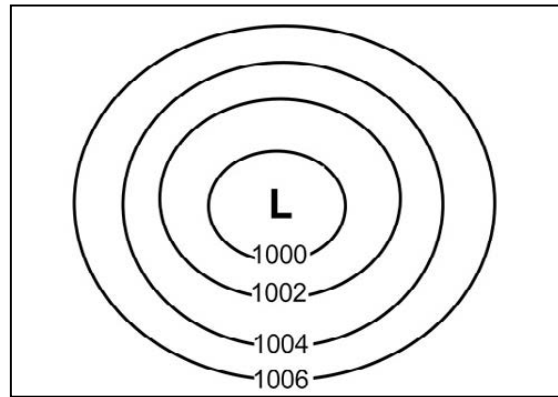
Importance and Key Terms

• Importance: Comprehending simple loci like circles aids in understanding complex shapes such as parabolas.
• Key Terms:
  • Equidistant: All points maintain the same distance from a central location, akin to the hands on a clock from its centre.
  • Points: Basic units that create a shape, similar to dots in a connect-the-dots activity.
  • Conditions: Specific criteria that outline the locus; such as circles arising from identical radii.

---

Understanding the Parabola as a Locus

Did you know that the reflective qualities of parabolas render them ideal for concentrating light beams in telescopes and vehicle headlights?

Parabola: A series of points equally spaced from a fixed point named the focus and a line known as the directrix. This mathematical concept facilitates the formation of parabolic shapes in satellite dishes to enhance signal concentration.

Key Components of a Parabola

• Focus: A specific point used as a reference to define the parabola. It relates to the convergence point in a satellite dish.
• Directrix: The straight line from which distances to the parabola's points are evaluated.
• Vertex: The nearest point on the parabola to the directrix.
• Axis of Symmetry: A line that passes through the focus and vertex, symmetrically dividing the parabola. Visualise it as splitting a dish into equal halves.

Detailed Explanation of Equidistance Property

• The parabolic form is characterised by this property of equidistance, similar to how a satellite dish deflects signals to the focus.
• Modifying the position of the focus or directrix changes the shape:
  • A closer focus results in a narrower parabola.
  • An extended focus leads to a broader one.

This can be visualised using reflection patterns within a dish.

Visualising a Parabola

• Symmetry denotes each side being a mirror image. Parabolas extend infinitely, open-ended.

"Refer to the diagram below" for a visual explanation:

Algebraic Representation

• Algebraically expressed as $y = ax^2 + bx + c$.
• Coefficient Effects:
  • a: Influences width and direction (upward if positive).
  • b: Shifts horizontally.
  • c: Moves vertically.

Diagrams and Illustrations

• The diagrams below depict key components:

"Observe the diagram below" regarding equidistance properties:

---

Deriving the Equation of a Parabola

Deriving the equation of a parabola is essential to understanding its geometric qualities, with practical origins in disciplines like physics and engineering. For instance, a parabola's form enables satellite dishes to optimise signal reception by focusing radio waves to a singular point.

Step-by-Step Derivation Guide

Establish the Definition

• Parabola: The locus of points consistently spaced from a focus and a directrix.
  • Focus: A given point, $F(h, k)$.
  • Directrix: A fixed line, $y = c$.

Algebraic Equations

1. Distance Formula Setup:
   • Determine distance from $(x, y)$ to the focus $(h, k)$:
     • $\sqrt{(x-h)^2 + (y-k)^2}$
   • Determine distance from $(x, y)$ to the directrix $y = c$:
     • $|y - c|$
2. Equalise Distances:
   • Equalise the two distances:
     • $\sqrt{(x-h)^2 + (y-k)^2} = |y - c|$

Simplification Process

1. Square Both Sides:

   • Eliminate radicals:
     • $(x-h)^2 + (y-k)^2 = (y-c)^2$

2. Simplify to Standard Form:

   • Reorganise to the standard form $y = ax^2 + bx + c$.

Highlight Common Pitfalls

• Sign errors: Errors frequently occur with negative terms during expansions.
• Algebraic expansion: Incorrect simplification leads to mistakes.

Tips to Avoid Errors:

• Reassess signs during procedures.
• Confirm each algebraic expansion step.

Practice and Reinforcement

Worked Example

Derive the equation of a parabola with a focus $(2, 3)$ and directrix $y = 1$:

• Step 1: Distance to focus:
  • $\sqrt{(x-2)^2 + (y-3)^2}$
• Step 2: Distance to directrix:
  • $|y-1|$
• Step 3: Equalise distances:
  • $\sqrt{(x-2)^2 + (y-3)^2} = |y-1|$
• Step 4: Square both sides and reorganise to obtain:
  • $y = 0.5x^2 - 2x + 4.5$

New Exercise

Try deriving the equation for a parabola with a focus $(1, -2)$ and directrix $y = -4$.

• Tip: Follow the procedural format from the example above.

Solution:

• Step 1: Distance to focus: $\sqrt{(x-1)^2 + (y+2)^2}$
• Step 2: Distance to directrix: $|y+4|$
• Step 3: Equalise distances: $\sqrt{(x-1)^2 + (y+2)^2} = |y+4|$
• Step 4: Square both sides: $(x-1)^2 + (y+2)^2 = (y+4)^2$ $(x-1)^2 + y^2+4y+4 = y^2+8y+16$ $(x-1)^2 = 4y+12$ $x^2-2x+1 = 4y+12$ $4y = x^2-2x-11$ $y = \frac{x^2-2x-11}{4}$

Key Takeaways and Tips

• Summary of Steps:

  • Specify the parabola definition.
  • Equalise the distance equations.
  • Square both sides and simplify to traditional form.

• Important Tips:

  • Ensure equations correlate with initial conditions.
  • Utilise diagrams for visual support.

---

Practice Problem Set

Comprehending parabolas as loci is integral for not only academic achievement but also for real-world applications. Parabolas frequently appear in technology, encompassing satellite communications, and in natural phenomena, like projectile motion in physics. Mastering these exercises sets a solid groundwork for more advanced concepts in mathematics and motivates ongoing learning.

• Problem 1: Basic Understanding of Locus

  • Description: Compute the locus of a point at equal distance from a focus at $(2, 3)$ and a line (directrix) $y = 1$. This is comparable to how a GPS identifies equidistant points.
  • Objective: Employ the distance formula to comprehend locus points.
  • Solution:
    • Equation: $(x - 2)^2 + (y - 3)^2 = (y - 1)^2$
    • Expand: $(x - 2)^2 + (y - 3)^2 = y^2 - 2y + 1$
    • Simplify to find: $y = \frac{1}{4}x^2 + 2x + \frac{15}{4}$

• Problem 2: Varying Directrix Positions

  • Description: Formulate the equation of a parabola with a focus at $(4, 7)$ and a horizontal directrix $y = 5$. Satellite dish designs utilise such parabolas for proper signal focus.
  • Objective: Visualise the impact of the directrix on the parabola's alignment and vertex.
  • Highlight: Concentrate on the critical steps in modifying focus and directrix conditions.
  • Solution:
    • Condition: The distance from $(x,y)$ to $(4,7)$ is equal to the distance to the line $y = 5$
    • Use the distance formula: $(x - 4)^2 + (y - 7)^2 = (y - 5)^2$
    • Solve to find: $y = \frac{1}{4}(x - 4)^2 + 5$

• Problem 3: Alternative Focus Positions

  • Description: Identify the equation of a parabola where the focus shifts to $(2, 1)$ and the directrix is $x = 0$.
  • Objective: Practice managing complex arrangements.
  • Solution:
    • Equation: $(x - 2)^2 + (y - 1)^2 = x^2$
    • Reorganise for $x$: $x = \frac{1}{2}y^2 + 2y + 2$
  • chatImportant

  Common mistakes include sign errors in calculations. :::

• Challenge Problem: Combine concepts from prior questions with a focus at $(1, -1)$ and directrix $x = -1$. This enhances an extensive understanding of the effects of focus and directrix changes on the parabola.

  • Solution:
    • Distance to focus: $\sqrt{(x-1)^2 + (y+1)^2}$
    • Distance to directrix: $|x+1|$
    • Equalise: $\sqrt{(x-1)^2 + (y+1)^2} = |x+1|$
    • Square both sides: $(x-1)^2 + (y+1)^2 = (x+1)^2$
    • Expand: $x^2-2x+1 + y^2+2y+1 = x^2+2x+1$
    • Simplify: $y^2+2y-4x = 0$
    • Rearrange: $x = \frac{y^2+2y}{4}$

Diagrams for Reference:

• 

---

Real-World Contextualisation

In exploring projectile motion, the trajectory often traces a parabolic path. Consider a ball launched at $45^\circ$ with an initial speed of 20 m/s:

• Objective: Compute both the apex (vertex) and where it descends using the focus-directrix link.
• Participating in simulations or constructing models can further elucidate these concepts and broaden comprehension.

Interactive Digital Exercises

• Employ tools such as GeoGebra to manipulate focus and directrix configurations and observe real-time transformations in parabolic shapes.
• Detailed Task Suggestions: Modify parameters like the directrix position and observe subsequent curvature changes.

Reference Tips for Mastery

• Comprehensive Checklist:

  • Validate proper setup of distance equations.
  • Accurately check all sign assignments in calculations.
  • Assure equations mirror anticipated parabolic geometry.

• Accentuate practical importance by demonstrating how these skills translate into fields such as engineering and physics, underscoring the practical merit of mastering this content.

Foster an iterative learning model by promoting repeated problem engagement, improving mastery through sustained practice.

---

Exam Tips

Understanding parabolas and their loci is pivotal not only for examination proficiency but also for practical implementation. Reflect on how parabolas contribute to satellite dish design and suspension bridge aesthetics, enhancing signal reception and structural elegance.

Strategy Tips

• Clear Diagram Labelling:

  • Diagram elements such as the focus, directrix, and vertex need clear labelling.
  • chatImportant

    Precise work guarantees partial credit. Ensure clear labelling.

  • Employ diagrams to depict a before-and-after view of accurate labelling techniques:

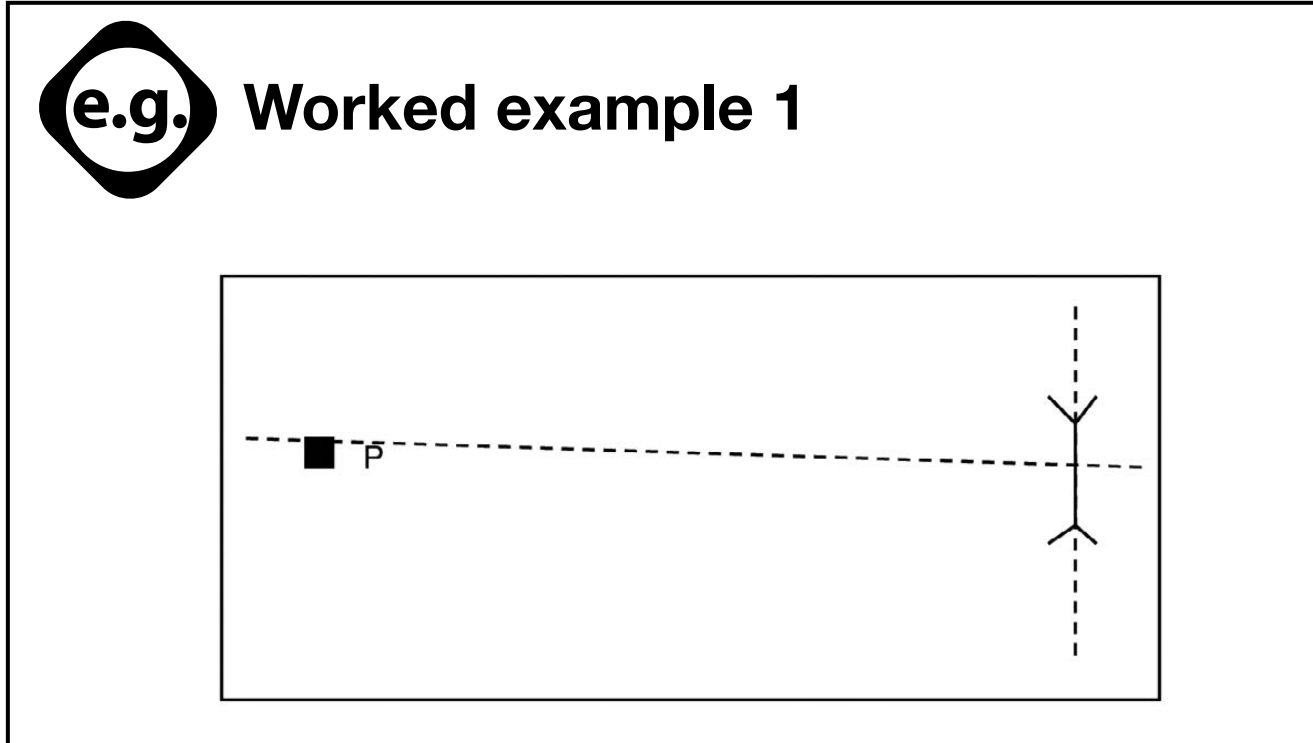
• Displaying Algebraic Work:

  • Present your work systematically for clarity and partial credit.
  • Acknowledge common algebraic pitfalls:
    • Incorrect operational signs.
    • Omitting vital steps in polynomial expansions.
    • Misinterpreting variable coefficients.
  • Highlight: A detailed understanding of algebraic steps ensures partial credit.
  • Use comparative tables to illustrate comprehensive step-by-step solutions:

Common Pitfalls

• Signs and Distance Calculations:
  • Elements to monitor:
    • Correct sign usage.
    • Accurate distance computations.
  • Use "SCADS" mnemonic for checks:
    • Symmetry
    • Consistent signs
    • Algebra accuracy
    • Distance verifications
    • Step verification
  • chatImportant

    Always reassess your sign usage and distance calculations in every step.

  • Illustrating pitfalls visually:

Final Advice

Steady verification fortifies learning and digital tool integration enriches study. Engage in self-evaluative sessions to better prepare for examinations efficiently.