Derivative Sign Analysis

Introduction to Derivatives

• A derivative quantifies the change in a function at a particular point.
• Real-world analogy: Similar to how speed reflects changes in position over time, a derivative quantifies a function's rate of change.
• Popular Misconception: Derivatives are not restricted to linear changes; they can describe intricate variations.

Notations for Derivatives

Enhanced Table of Notations

Notation	Name	Usage Context	Special Notes
$f'(x)$	Lagrange's Notation	Single function derivatives	Most straightforward representation
$\frac{dy}{dx}$	Leibniz's Notation	Differential processes in equations	Highlights differentiation processes
$Df(x)$	Operator Notation	Functional Analysis	Useful in variable-independent contexts

Graphical Representation of Derivatives

• Tangent Lines: The slope of the tangent line at any point is equal to the derivative at that point.
• Slope Interpretations:
  • A positive slope indicates that the function is increasing.
  • A negative slope signifies that the function is decreasing.
  • A zero slope represents a level point where the rate of change briefly ceases.

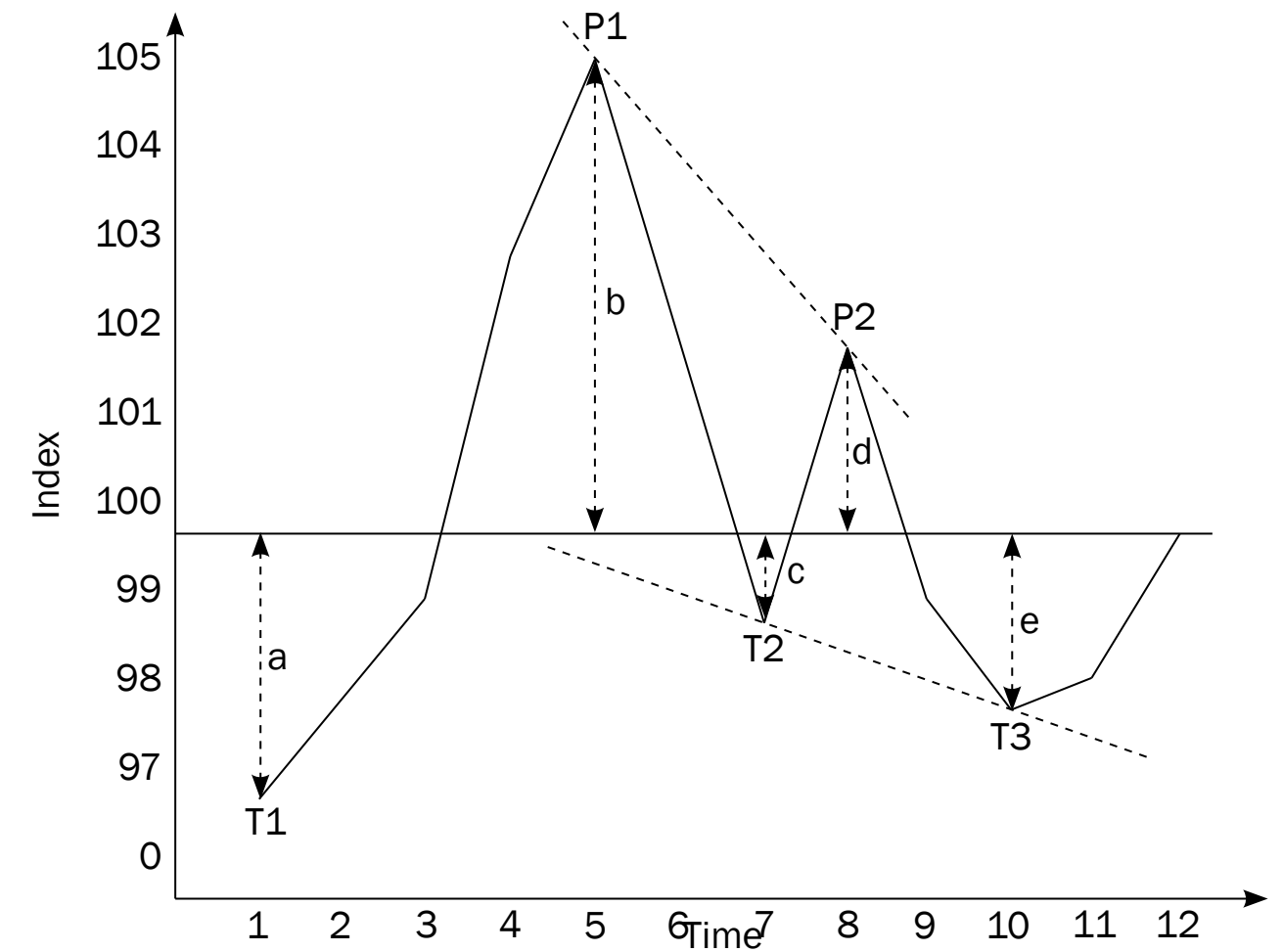
Derivative's Role in Function Analysis

Increasing/Decreasing Analysis

• Increasing $f(x)$: Occurs where $f'(x) > 0$ — the function rises.
• Decreasing $f(x)$: Where $f'(x) < 0$ — the function descends.
• Stationary Points: Occur at $f'(x) = 0$, signifying possible extrema or points of inflection.

Interval Analysis

Calculation Process

1. Calculate the first derivative $f'(x)$.
2. Identify critical points by setting $f'(x) = 0$.
3. Determine intervals defined by these critical points.
4. Use Test Points to evaluate the sign of $f'(x)$ in each interval.

Common Misconceptions

Misconception: Uniform Behaviour Assumption

Zero Derivatives

• Scenario: Present at points where the function neither increases nor decreases — potentially indicating stationary points.
• Important Callout: It is crucial to recall that stationary points are not always maxima or minima without further detailed analysis.

Example Problems and Solutions

Example 1: Determine the behaviour of $f(x) = x^3 - 3x + 1$.

1. Find $f'(x) = 3x^2 - 3$.

2. Solve for stationary points: $3x^2 - 3 = 0$ $3(x^2 - 1) = 0$ $x^2 = 1$ $x = 1$ or $x = -1$

3. Analyse intervals:

   • For $x < -1$: Test $x = -2$, $f'(-2) = 3(4) - 3 = 9 > 0$, so $f(x)$ is increasing
   • For $-1 < x < 1$: Test $x = 0$, $f'(0) = -3 < 0$, so $f(x)$ is decreasing
   • For $x > 1$: Test $x = 2$, $f'(2) = 3(4) - 3 = 9 > 0$, so $f(x)$ is increasing

Therefore: $f(x)$ increases when $x < -1$ or $x > 1$, and decreases when $-1 < x < 1$.

Example 2: Analyse $h(x) = x^2 - 4x$.

1. Calculate $h'(x) = 2x - 4$.

2. Determine critical point by setting $h'(x) = 0$: $2x - 4 = 0$ $2x = 4$ $x = 2$

3. Interval analysis:

   • For $x < 2$: Test $x = 1$, $h'(1) = 2(1) - 4 = -2 < 0$, so $h(x)$ is decreasing
   • For $x > 2$: Test $x = 3$, $h'(3) = 2(3) - 4 = 2 > 0$, so $h(x)$ is increasing

Therefore: $h(x)$ decreases when $x < 2$ and increases when $x > 2$. The function has a minimum at $x = 2$.

Graphical Techniques

• Visual Learning: Vital for grasping the concepts of derivatives. Transform abstract ideas into more concrete forms using graphs.
• Tables and Plotting: Construct tables of values for derivative calculations and graph plotting.

---

Through these detailed analyses, we can understand the complex behaviours of functions and the vital role derivatives play in comprehending these dynamics.