Venn Diagrams and Probability

Introduction to Venn Diagrams

Venn diagrams are essential tools for visualising set relationships and simplifying complex theories. They are especially useful in applications such as probability, where they convert abstract ideas into practical problem-solving aids. Everyday decision-making processes often benefit from the clarity that Venn diagrams offer.

Key Terminology

• Intersection (A ∩ B): The common elements found in both sets A and B.
• Union (A ∪ B): The combined area encompassing all elements from sets A and B.
• Complement (A'): Elements that exist outside set A.

Visualisation and Examples

Scenario Exploration

Consider a group of students participating in different sports:

• Football
• Basketball
• Swimming

In this class, some students have overlapping interests, which can be effectively represented using a Venn diagram. This diagram aids in visualising distinct and shared participation.

Problem Walkthrough

A class of 30 students has varying sports interests: 12 play football, 18 play basketball, and 5 swim. Using a Venn diagram, determine:

• The number of students involved in both football and basketball.
• Those who engage in all three sports.

Let's solve this step by step:

1. Draw a Venn diagram with three overlapping circles for football (F), basketball (B), and swimming (S).
2. We know total students = 30, football = 12, basketball = 18, swimming = 5.
3. Let's denote the overlap between football and basketball as x.
4. Let's denote the students in all three sports as y.
5. To find x (football and basketball overlap), we need to use the formula: $n(F) + n(B) - n(F \cap B) = n(F \cup B)$ This means that $12 + 18 - x =$ the total students in either sport.
6. Assuming there are z students who don't participate in any sport, we can write: $n(F \cup B \cup S) + z = 30$

To complete the solution, we would need more information, but the approach demonstrates how to systematically solve such problems using Venn diagrams.

Addressing Misconceptions

Misunderstandings often arise, such as confusing:

• Union for Intersection
• Interpretation of complements

Use annotated diagrams to clearly illustrate errors and correct understanding, focusing on the effective use of digital or physical tools to engage students interactively.

Multi-Stage Experiments Using Venn Diagrams

Overview

Multi-stage experiments are processes where each step influences subsequent events. They are crucial for understanding how probabilities evolve based on earlier occurrences. Venn diagrams simplify these sequences by visually representing overlapping events.

Representation of Multi-Stage Probabilities

• Circles as Events: Each circle in a Venn diagram represents a distinct event.
• Overlaps and Unions:
  • Overlaps indicate intersections (shared outcomes between events).
  • Unions depict combined outcomes (either/or situations).

Example: Basketball Tournament

Consider a basketball tournament:

• Stages: Quarter-finals, Semi-finals, Finals.
• Use diagrams to show how winning early stages affects final outcomes.

Step-by-Step Example

Imagine a basketball tournament:

• Define Stages: Quarter-finals, Semi-finals, Finals
• Calculate Probabilities:
  • Probability of winning Semi-finals and then Finals.
  • Display intersections (reached both Semi-finals and Finals) and unions (won either Semi-finals or Finals) using Venn diagrams.

These calculations demonstrate how initial successes impact later event probabilities.

Clarifications and Common Issues

Misconceptions:

• Confusing mutually exclusive events with overlapping ones.
• Ensure accuracy in Venn diagram sections.

Combining Venn Diagrams with Tree Diagrams

• Tree diagrams: Useful for illustrating sequential events.
• Combined with Venn diagrams, they enhance understanding.

Case Study: Utilise both diagrams for strategic planning in sports events, illustrating how early victories impact later stages.

Introduction to Probability Scale

• 0 (Impossible): The event will not occur under any circumstances.
• 0.2 (Unlikely): The event is not expected to happen.
• 0.5 (Even Chance): Equal probability of occurring or not.
• 0.8 (Likely): The event is expected to occur.
• 1 (Certain): The event is assured to happen.

Visualisation Through Diagrams

• Diagrams can depict probability levels from impossible (0) to certain (1).
• Weather forecasts (e.g., 30% chance of rain) and rolling a die (e.g., 1/6 chance of any face) on the probability scale.
• Diagrams with annotations support visual comprehension.

Common Misconceptions

• 'Likely' vs 'Certain': "Likely" implies a high probability, not guaranteed certainty.
  • Example: An 80% chance of rain is considered likely but not certain.
• 'Unlikely' vs 'Impossible': "Unlikely" events can still happen, unlike impossible ones.
  • Real-world analogy: Winning a lottery is unlikely, but not impossible.

Probability in Everyday Language

• Everyday expressions related to probability values.
  • "Highly improbable" = 0.1 (e.g., snowing in summer in London)
  • "Fair chance" = 0.5 (e.g., flipping a coin)
  • "Pretty likely" = 0.7 (e.g., tram arriving on time)

Expression	Probability Value
Highly Improbable	0.1
Fair Chance	0.5
Pretty Likely	0.7

Practice Problems

• Problem 1: Determine the probability of drawing a heart from a standard deck.
  • Hint: Total hearts = 13.
  • Solution: Probability = $\frac{13}{52} = 0.25$. This is an unlikely event.
• Problem 2: The Met Office predicts a 70% chance of sunshine tomorrow.
  • Hint: Convert percentage to probability.
  • Solution: Probability = 0.7, indicating it is pretty likely.

Visual Clarifications

• Create custom diagrams, like drawing coloured balls from a bag, to explore probabilities.
• Interactive Diagrams: Use digital tools allowing slider manipulation to observe visual probability changes.

Probabilistic Thinking

• Developing probabilistic thinking
  is crucial for informed daily decision-making.
  • Examples: Deciding to take an umbrella based on weather forecasts, choosing clothing according to the weather.
• Effectively assess risks and benefits by applying calculated probabilities.

Introduction to Set Language and Notation

Understanding set language and notation is key when tackling probability problems, allowing for organised and efficient problem-solving.

• Example: In a club scenario, students in either basketball or swimming clubs—or both.

• Example: Students engaged in both basketball and swimming fall within the intersection.

• Example: Students who are not part of the basketball club.

Elaborating Set Notation in Problems

• Terms and Definitions:
  • "A and B" = Intersection
  • "A or B" = Union
  • "Not A" = Complement

Step-by-Step Guide:

• Problem: Determine the number of students who belong to either club or both using a Venn diagram.
  • Step 1: Draw circles for basketball and swimming clubs.
  • Step 2: Highlight overlap for students in both clubs.
  • Step 3: Count total members from both sets.

Key Probability Rules

Understanding the Complement Rule

• Formula: $$P(A') = 1 - P(A)$$
  • Context: If 70% are in a club, then 30% are not.

Applying the Addition Rule

• For non-mutually exclusive events:

  $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$
  • Context: Total probability includes subtraction of overlap (intersection).

Common Pitfalls

Simulation and Trials in Probability

Introduction to Simulations and Trials

Simulations in Probability:

• Objective: Model complex systems with computers or physical components.
• Facilitate probability estimation when theoretical formulas are complicated.

Importance:

• Transform real-life scenarios into manageable models.
• Deliver quick results without exhaustive computations.

Common Simulation Methods

Physical Simulations:

• Types include:
  • Dice rolls
  • Coin flips
  • Card draws

Digital Simulations:

• Benefits:
  • Precision
  • Flexibility
  • Reduced biases

Reproducibility in Probability Experiments

Concept:

• Achieving consistent outcomes across multiple trials.
• Critical for verifying experimental results.

Best Practices:

• Documentation: Clearly document each step.
• Consistent Setup: Maintain identical conditions for every trial.
• Verification Tools: Employ established software for results confirmation.

Interactive Example Activity

Multi-Stage Simulation Activity:

• Stage 1: Roll two dice.
• Stage 2: Calculate the sum.
• Stage 3: Determine the progression based on sum outcomes.

Probability Calculation:

• Example: $P(\text{sum} = 7) = \frac{6}{36} = \frac{1}{6}$

Worked Example:

• Calculate the probability for reaching a specific condition.
• E.g., rolling a sum of 7, then reaching another condition.
• Offer structured steps with outcomes:
  • Roll: Outcome 7
  • Next Steps: Follow probability steps for new conditions.

Challenges and Solutions in Simulations

Common Issues:

• Biases observed in physical simulations.
• Digital Solutions: Offer precision and bias elimination.

Error Analysis:

• Identify and rectify inconsistencies.
• Use statistical techniques for accurate corrections.

Definition of Relative Frequency

Relative Frequency: the ratio of favourable outcomes to the total number of trials conducted.

• Utilised for estimating probability when theoretical models are absent or impractical.

Example Using Frequency Tables

Consider a typical dice-rolling experiment:

• Step 1: Roll a 6-sided die 60 times.
• Step 2: Record outcomes for each result.
• Step 3: Determine the frequency of a specific result, such as rolling a '3' ten times.
• Step 4: Calculate relative frequency:
  • Number of '3' outcomes = 10
  • Total trials = 60
  • Relative Frequency = $\frac{10}{60} = 0.1667$

Outcome	Frequency
1	9
2	8
3	10
4	12
5	11
6	10

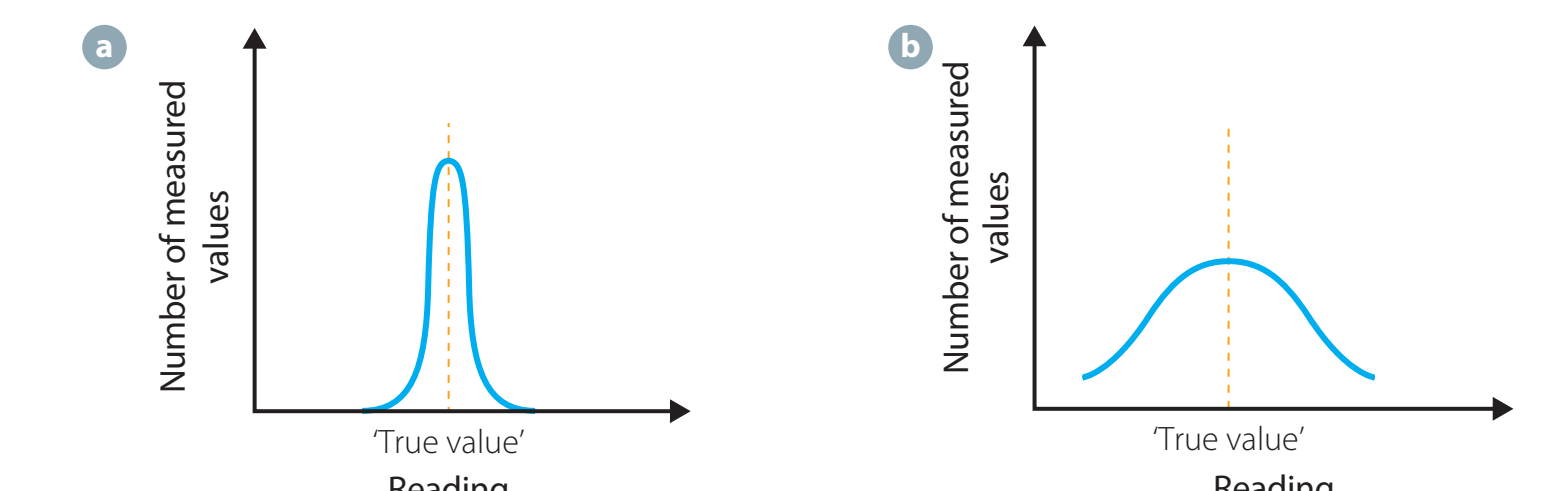
Contrasting Theoretical Probability vs. Relative Frequency

• Theoretical Probability:

  • Assumes optimal outcomes in a controlled model.
  • Example: Probability of any specific die face = $\frac{1}{6}$.

• Relative Frequency:

  • Based on observed experimental outcomes.
  • Shows deviations initially but trends toward theoretical predictions with more trials.

Classroom Applications

• Relatable Exercise: Calculate personal probabilities of punctuality.

  • Example:
    • Late 5 out of 20 days:
    • Relative Frequency = $\frac{5}{20} = 0.25$.

Simulated Data Conversion

Interactive Scenario:

• Start a dice game simulation.
• Predict frequency outcomes and potential results.
• Record and summarise observations.

Through these exercises, learners can bridge theoretical constructs with practical insights, relating real-world experiences to reflective learning.

---

Understanding Misconceptions

• Students frequently make errors using Venn diagrams in probability calculations, particularly concerning intersections and unions.
  • Intersection Overcounting:
    • Definition: Intersection (A ∩ B) constitutes elements shared between sets.
    • Common Error: Incorrectly adding probabilities of sets and their intersection, leading to overcounting.
    • Example:
      • Incorrect: $P(A) + P(B) + P(A \cap B)$.
      • Correct: $P(A) + P(B) - P(A \cap B)$.
    • Visual Aid: Refer to the diagram below for clear understanding.
      • 

Union vs. Intersection

• Definitions:
  • Union (A ∪ B): Encompasses elements in at least one set.
  • Intersection (A ∩ B): Consists of common elements in both sets.
• Common Misunderstanding:
  • Students often confuse A ∪ B with A ∩ B, resulting in calculation errors.
• Scenario:
  • Confusing $A \cup B$ with $A \cap B$ impacts results.
  • Visual Clarification:
    • Consult interactive diagrams to address confusion.
    • 

Visual Tools and Corrective Measures

• Annotated Diagrams:
  • Highlight and rectify common errors.
• Editable Diagrams:
  • Utilise digital tools for Venn diagrams offering real-time feedback.

Problem-Solving with Visual Clarifications

• Step-by-step Solutions:
  • Split complex problems into manageable visual steps.
  • 

Feedback Loop & Iterations

• Interactive Learning:
  • Employ tools delivering real-time feedback.
  • Example of an instant feedback platform.
  • 

---