Photo AI
In the diagram, AED and ABC are straight lines and BE is parallel to CD - OCR - GCSE Maths - Question 13 - 2020 - Paper 6
Question 13
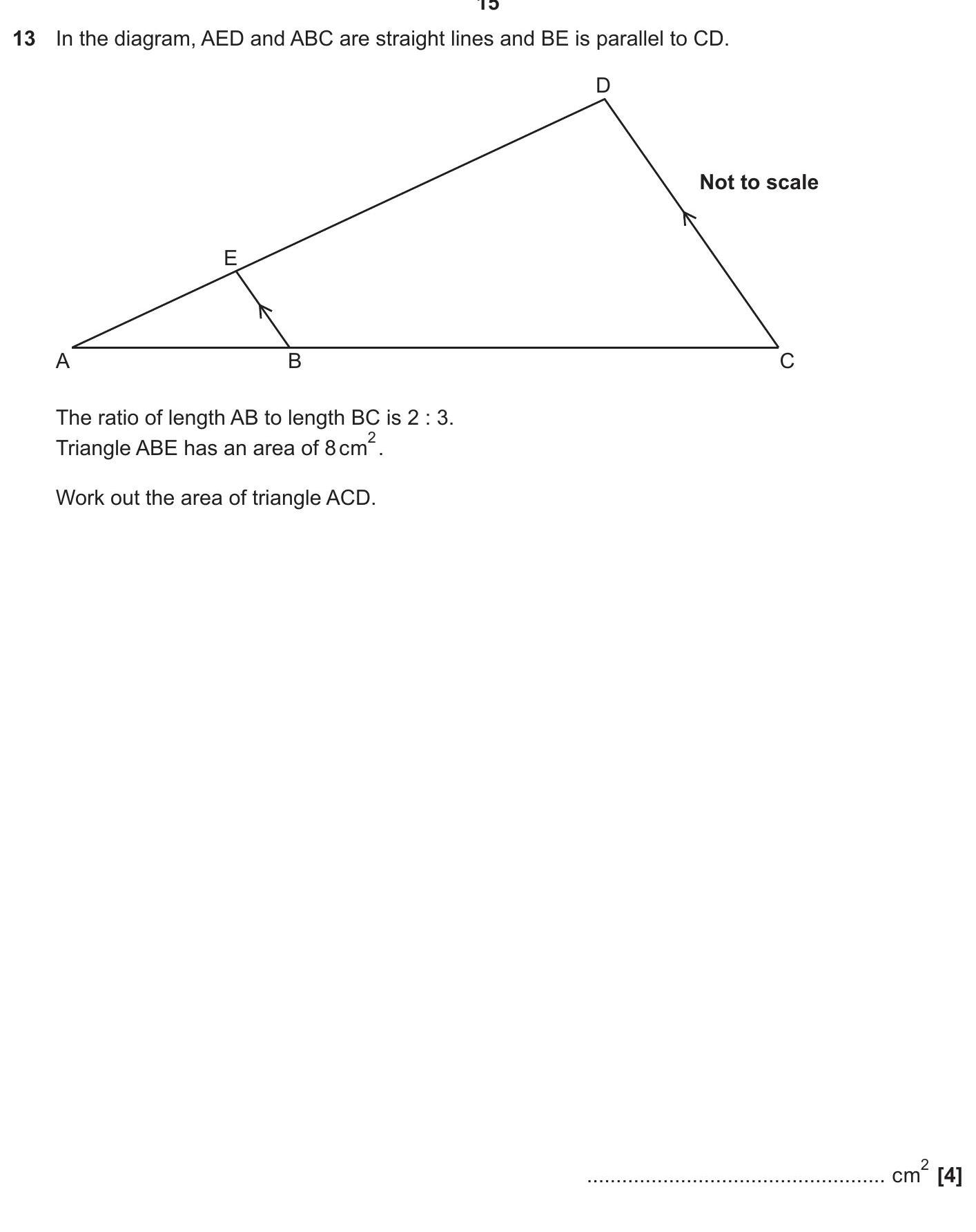
In the diagram, AED and ABC are straight lines and BE is parallel to CD. The ratio of length AB to length BC is 2 : 3. Triangle ABE has an area of 8 cm². Work out ... show full transcript
Worked Solution & Example Answer:In the diagram, AED and ABC are straight lines and BE is parallel to CD - OCR - GCSE Maths - Question 13 - 2020 - Paper 6
Step 1
Calculate the Ratio of Areas
Answer
Since BE is parallel to CD, triangles ABE and ACD are similar. The ratio of their areas is equal to the square of the ratio of their corresponding sides. Given that the ratio of length AB to BC is 2 : 3, the total length AC is AB + BC. Therefore, we have:
Now, the area ratio can be calculated:
ext{Area ratio} = rac{AB^2}{AC^2} = rac{(2)^2}{(5)^2} = rac{4}{25}
Step 2
Determine the Area of Triangle ACD
Answer
If the area of triangle ABE is 8 cm², we can denote the area of triangle ACD as A_ACD. Using the area ratio:
Substituting the known area of triangle ABE:
Cross-multiplying gives:
Dividing both sides by 4 results in:
Therefore, the area of triangle ACD is 50 cm².
