Photo AI
The graph of \( y = -x^2 - 9 \) is shown below - AQA - A-Level Maths Mechanics - Question 1 - 2019 - Paper 3
Question 1
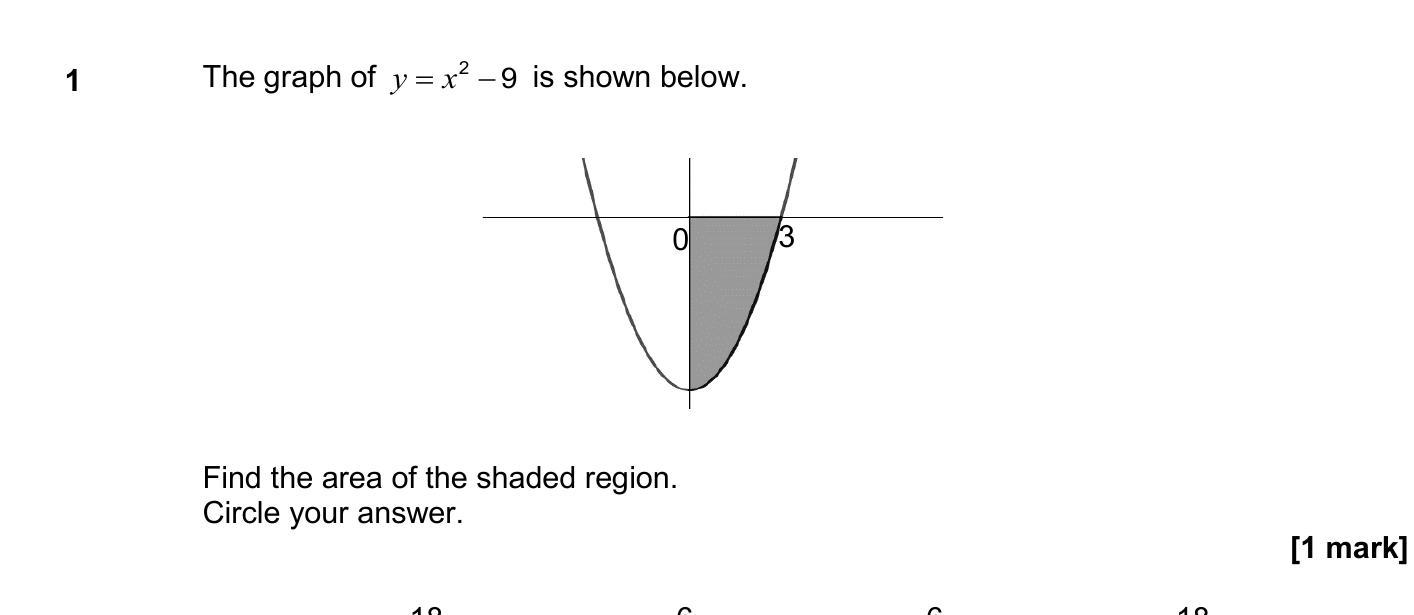
The graph of \( y = -x^2 - 9 \) is shown below. Find the area of the shaded region. Circle your answer.
Worked Solution & Example Answer:The graph of \( y = -x^2 - 9 \) is shown below - AQA - A-Level Maths Mechanics - Question 1 - 2019 - Paper 3
Step 1
Find the area of the shaded region.
Answer
To find the area of the shaded region, we first need to determine the points where the parabola intersects the x-axis. This can be done by setting ( y = 0 ):
[ 0 = -x^2 - 9 ]
This means we rearrange and find: [ -x^2 = 9 ] [ x^2 = -9 ]
This shows that the parabola does not intersect the x-axis. The area we are interested in is actually the region above ( y = -9 ) and below the parabola.
Next, we find the vertex of the parabola, which occurs at ( x = 0 ), giving:
[ y = -0^2 - 9 = -9 ]
Now we integrate to find the area of the shaded region between the x-values of -3 and 3, which are the points at which ( y = -9 ):
[ Area = \int_{-3}^{3} (-x^2 - 9) , dx ]
Calculating the integral:
[ = \left[ -\frac{x^3}{3} - 9x \right]_{-3}^{3} ]
Evaluating this:
[ = \left( -\frac{(3)^3}{3} - 9(3) \right) - \left( -\frac{(-3)^3}{3} - 9(-3) \right) ] [ = \left( -9 - 27 \right) - \left( -(-9) + 27 \right) ] [ = (-36) - (-36) ] [ = 36 ]
Thus, the area of the shaded region is ( 18 ) square units. The answer to circled part is ( 18 ).
