Photo AI
A teacher is selected at random - AQA - A-Level Maths Mechanics - Question 13 - 2020 - Paper 3
Question 13
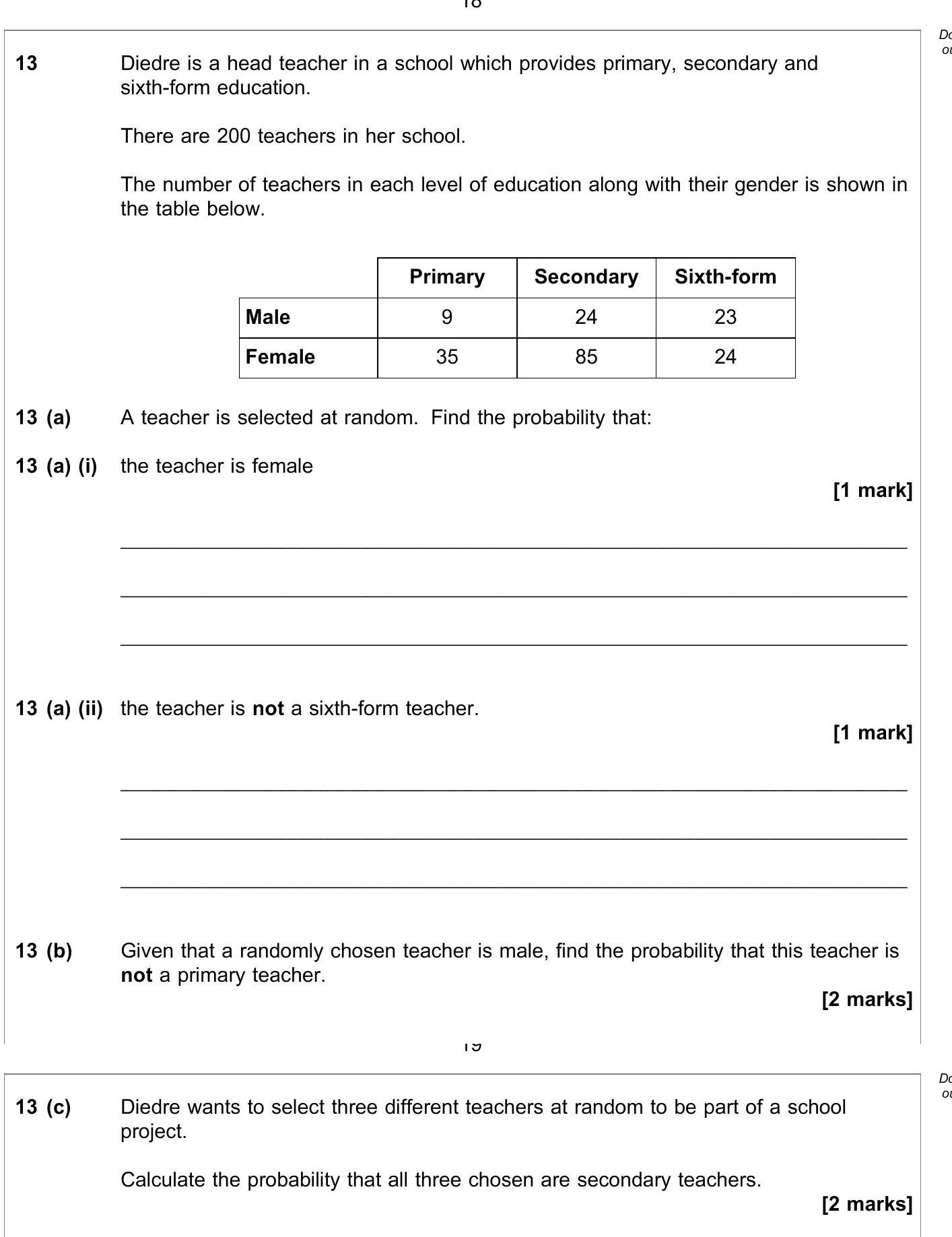
A teacher is selected at random. Find the probability that: (i) the teacher is female (ii) the teacher is not a sixth-form teacher. (b) Given that a randomly chos... show full transcript
Worked Solution & Example Answer:A teacher is selected at random - AQA - A-Level Maths Mechanics - Question 13 - 2020 - Paper 3
Step 1
the teacher is female
Answer
To find the probability that a randomly selected teacher is female, we first need to determine the total number of female teachers.
From the table:
- Primary: 35
- Secondary: 85
- Sixth-form: 24
Total female teachers = 35 + 85 + 24 = 144.
The total number of teachers is 200.
Thus, the probability that the teacher is female is given by:
Step 2
the teacher is not a sixth-form teacher.
Answer
To find the probability that the teacher is not a sixth-form teacher, we need to first find the number of teachers who are not in the sixth-form category.
The total number of sixth-form teachers is:
- Male: 23
- Female: 24
Hence, total sixth-form teachers = 23 + 24 = 47.
Therefore, the number of teachers not in the sixth-form = 200 - 47 = 153.
Now, the probability is:
Step 3
Given that a randomly chosen teacher is male, find the probability that this teacher is not a primary teacher.
Answer
We start by finding the total number of male teachers:
- Primary: 9
- Secondary: 24
- Sixth-form: 23
Total male teachers = 9 + 24 + 23 = 56.
To find those who are not in primary, we subtract the number of primary male teachers:
Total male not primary = 24 + 23 = 47.
Hence, the conditional probability is:
Step 4
Calculate the probability that all three chosen are secondary teachers.
Answer
To find the probability that all three randomly chosen teachers are secondary teachers, we first determine the total number of secondary teachers:
- Male: 24
- Female: 85
Total secondary teachers = 24 + 85 = 109.
Now, the probability that all three chosen teachers are secondary is given by:
Calculating this gives:
Thus, the final answer is approximately 0.16.
