Photo AI
y = \frac{1}{x^2} Find an expression for \(\frac{dy}{dx}\) - AQA - A-Level Maths Mechanics - Question 1 - 2018 - Paper 1
Question 1
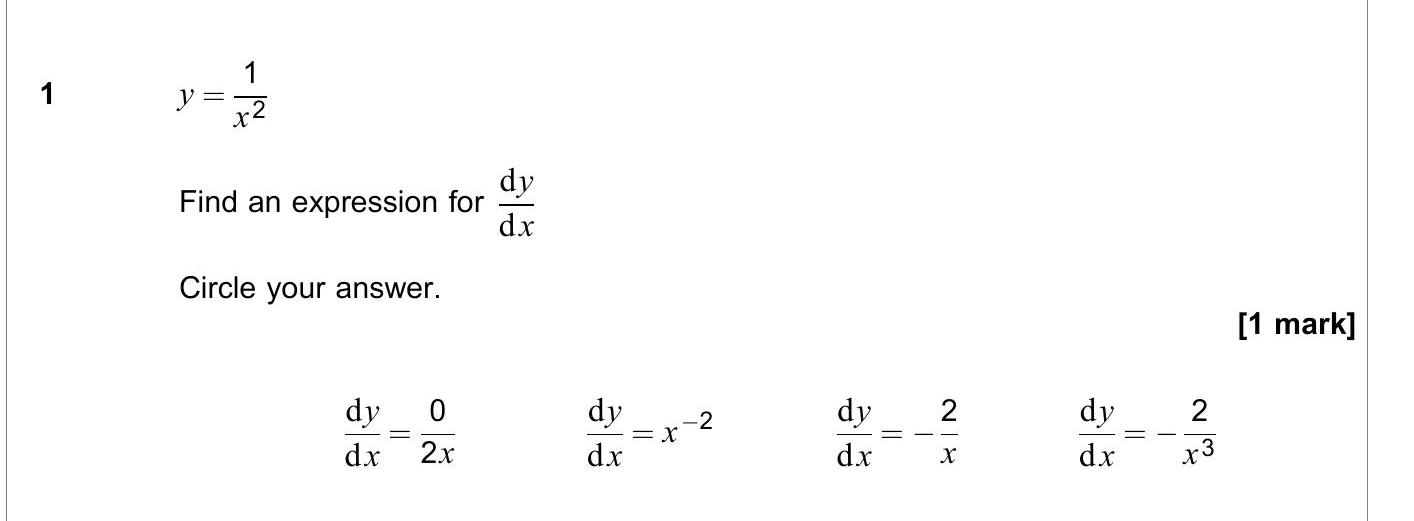
y = \frac{1}{x^2} Find an expression for \(\frac{dy}{dx}\). Circle your answer.
Worked Solution & Example Answer:y = \frac{1}{x^2} Find an expression for \(\frac{dy}{dx}\) - AQA - A-Level Maths Mechanics - Question 1 - 2018 - Paper 1
Step 1
Find an expression for \(\frac{dy}{dx}\)
Answer
To find the derivative of (y = \frac{1}{x^2}), we can apply the power rule of differentiation.
-
Rewrite the function: [ y = x^{-2} ]
-
Differentiate using the power rule: [ \frac{dy}{dx} = -2x^{-3} ]
-
Rewrite the answer in a more standard form: [ \frac{dy}{dx} = -\frac{2}{x^3} ]
Therefore, the expression for (\frac{dy}{dx}) is ( -\frac{2}{x^3} ).
