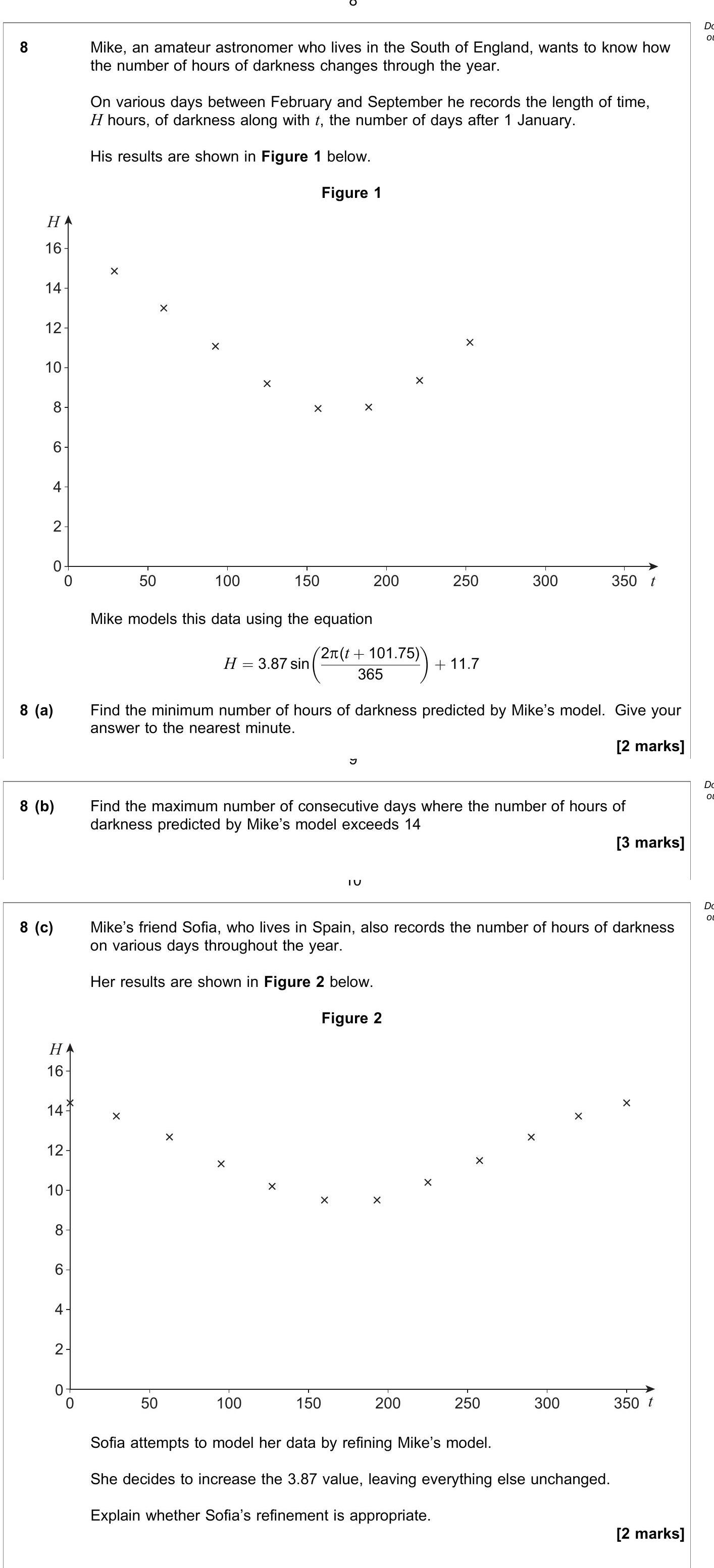
Mike, an amateur astronomer who lives in the South of England, wants to know how the number of hours of darkness changes through the year - AQA - A-Level Maths Mechanics - Question 8 - 2020 - Paper 1

Set the equation for H greater than 14:

$3.87 \, ext{sin} \left( \frac{2\pi(t + 101.75)}{365} \right) + 11.7 > 14$

This simplifies to:

$3.87 \, ext{sin} \left( \frac{2\pi(t + 101.75)}{365} \right) > 2.3$

Dividing through by 3.87, we get:

$\text{sin} \left( \frac{2\pi(t + 101.75)}{365} \right) > 0.593$

Finding the angles related to this sine value gives:

$\frac{2\pi(t + 101.75)}{365} = arcsin(0.593)$

Calculating gives values of approximately ( t \approx 300.22 ) and ( t \approx 408.77 ).

Thus, the consecutive days can be calculated as:

$\text{Days} = 408 - 300 = 108 \text{ days}$.

Sofia's refinement aims to increase the amplitude of the graph by raising the 3.87 value in Mike's model. While this would increase the range of the graph and the variability in darkness hours, Sofia's data does not suggest such fluctuations. Thus, her refinement may not be appropriate, as it could misrepresent the relatively stable trend in her recorded hours of darkness, leading to a less accurate model.