Photo AI
8 (a) Prove the identity $$\frac{\sin 2x}{1 + \tan^2 x} = 2 \sin x \cos^3 x$$ 8 (b) Hence find $$\int \frac{4 \sin 4\theta}{1 + \tan^2 2\theta} d\theta$$ - AQA - A-Level Maths Mechanics - Question 8 - 2018 - Paper 3
Question 8
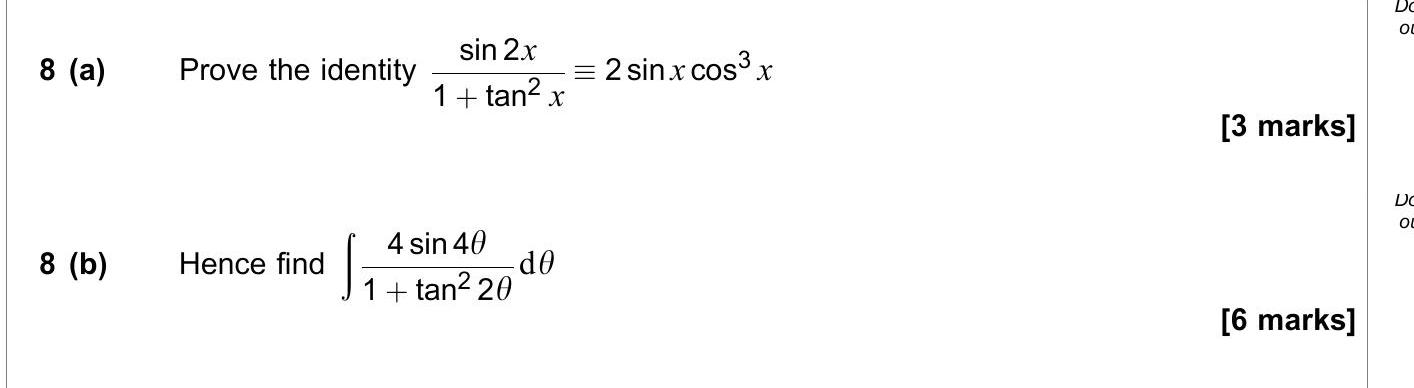
8 (a) Prove the identity $$\frac{\sin 2x}{1 + \tan^2 x} = 2 \sin x \cos^3 x$$ 8 (b) Hence find $$\int \frac{4 \sin 4\theta}{1 + \tan^2 2\theta} d\theta$$
Worked Solution & Example Answer:8 (a) Prove the identity $$\frac{\sin 2x}{1 + \tan^2 x} = 2 \sin x \cos^3 x$$ 8 (b) Hence find $$\int \frac{4 \sin 4\theta}{1 + \tan^2 2\theta} d\theta$$ - AQA - A-Level Maths Mechanics - Question 8 - 2018 - Paper 3
Step 1
Prove the identity
Answer
To prove the identity, we start by examining the left-hand side:
We can use the identity for ( \sin 2x = 2 \sin x \cos x ) to rewrite the numerator:
Next, using the identity ( \tan^2 x = \frac{\sin^2 x}{\cos^2 x} ), we have:
Thus, we can rewrite the denominator as:
This shows that:
Now, for the right-hand side:
Since both sides are equal, we conclude that:
Step 2
Hence find
Answer
Using the identity proven in part (a), we rewrite the integral:
Using the identity , we can simplify the denominator:
Thus, we can express this as:
Now substituting:
Next, we can use the substitution, letting ( u = \cos 2\theta ), then ( du = -2 \sin 2\theta d\theta ), which converts the integral to:
