Photo AI
A curve has equation $y = x^5 + 4x^3 + 7x + q$ where $q$ is a positive constant - AQA - A-Level Maths Mechanics - Question 2 - 2018 - Paper 3
Question 2
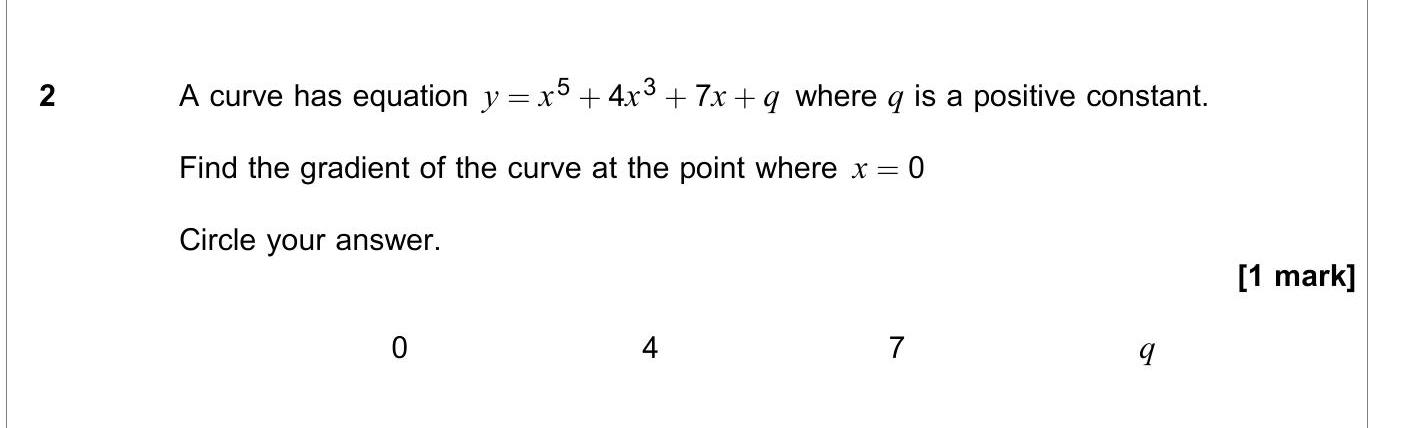
A curve has equation $y = x^5 + 4x^3 + 7x + q$ where $q$ is a positive constant. Find the gradient of the curve at the point where $x = 0$. Circle your answer.
Worked Solution & Example Answer:A curve has equation $y = x^5 + 4x^3 + 7x + q$ where $q$ is a positive constant - AQA - A-Level Maths Mechanics - Question 2 - 2018 - Paper 3
Step 1
Find the gradient of the curve at the point where $x = 0$
Answer
To find the gradient of the curve, we first need to calculate the derivative of the function with respect to .
The function is given by:
Taking the derivative, we get:
Next, we substitute into the derivative to find the gradient at that point:
Thus, the gradient of the curve at the point where is . Therefore, we circle the answer: 7.
