Photo AI
Given that $y = ext{ln}(5x)$ find \frac{dy}{dx} - AQA - A-Level Maths Mechanics - Question 2 - 2021 - Paper 1
Question 2
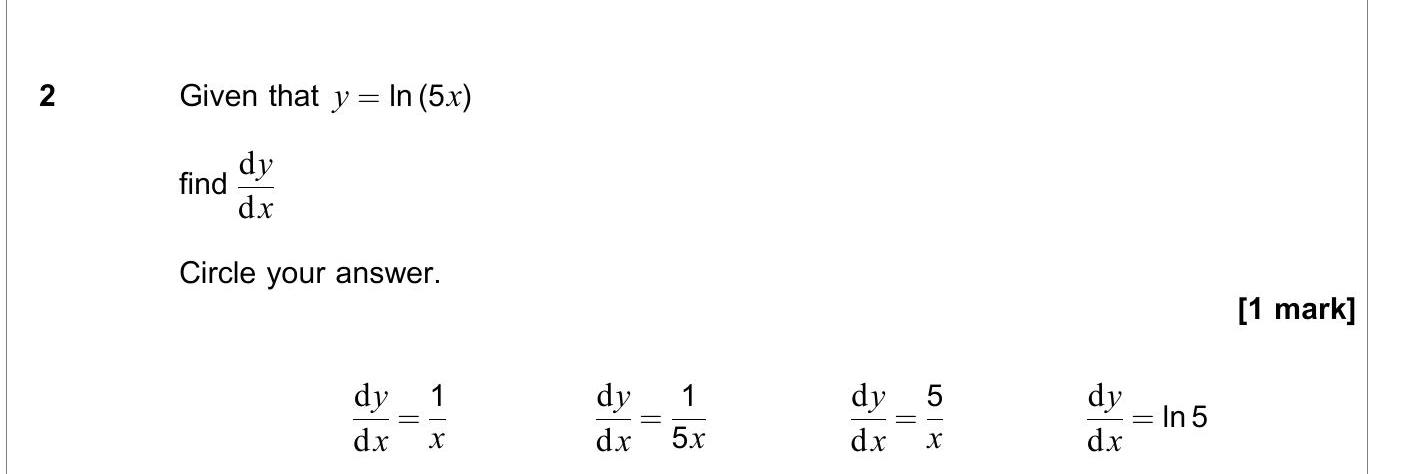
Given that $y = ext{ln}(5x)$ find \frac{dy}{dx}. Circle your answer.
Worked Solution & Example Answer:Given that $y = ext{ln}(5x)$ find \frac{dy}{dx} - AQA - A-Level Maths Mechanics - Question 2 - 2021 - Paper 1
Step 1
