Photo AI
A uniform rod, AB, has length 4 metres - AQA - A-Level Maths Mechanics - Question 11 - 2018 - Paper 2
Question 11
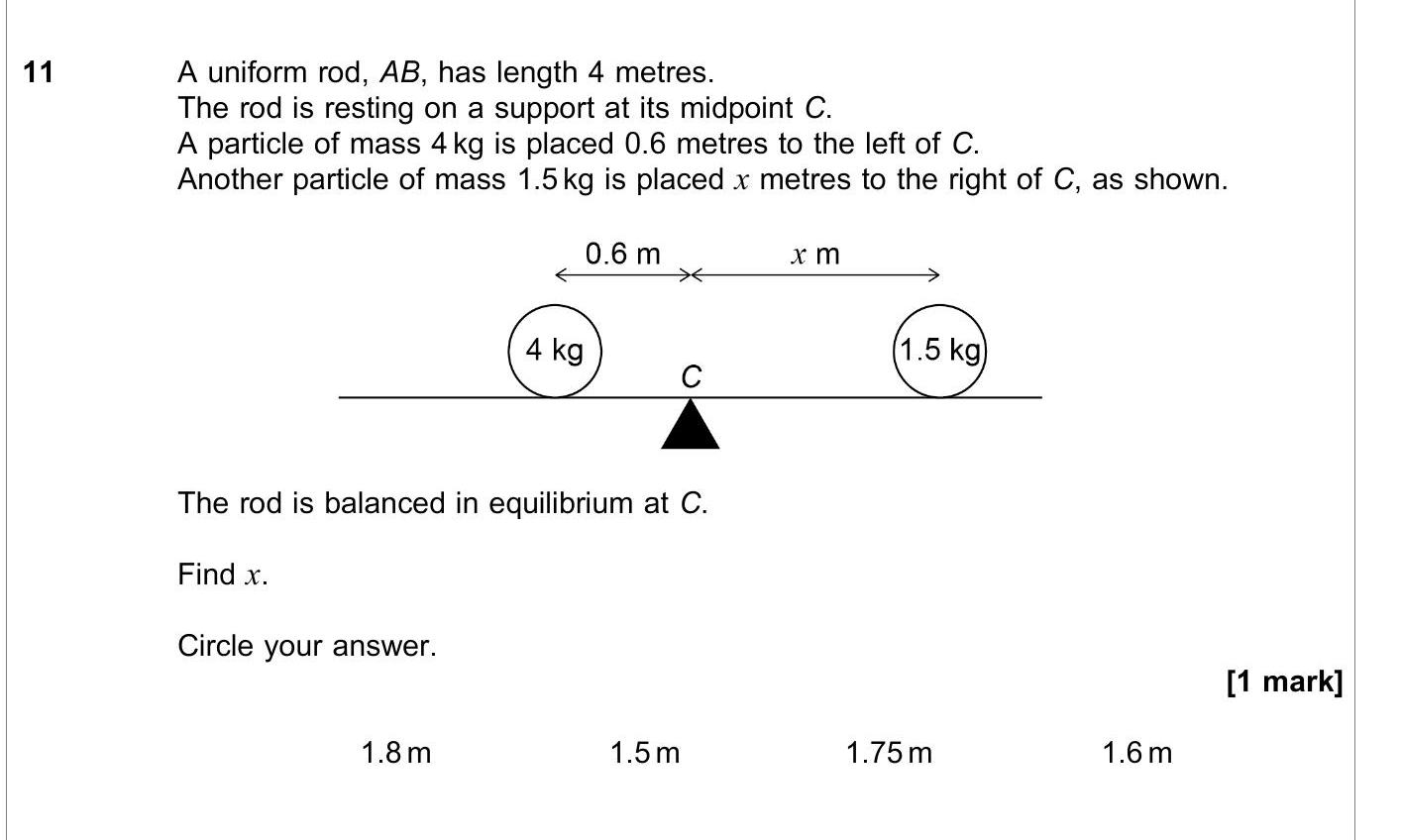
A uniform rod, AB, has length 4 metres. The rod is resting on a support at its midpoint C. A particle of mass 4 kg is placed 0.6 metres to the left of C. Another par... show full transcript
Worked Solution & Example Answer:A uniform rod, AB, has length 4 metres - AQA - A-Level Maths Mechanics - Question 11 - 2018 - Paper 2
Step 1
Find x.
Answer
To find the value of x where the rod is balanced in equilibrium at point C, we will apply the principle of moments, which states:
The sum of clockwise moments about a point equals the sum of counterclockwise moments about that point.
-
Identify the moments:
-
Moment caused by the 4 kg mass: The force due to the 4 kg mass is calculated as:
\text{Force} = mass \times gravity = 4 \text{ kg} \times 9.81 \text{ m/s}^2 \approx 39.24 \text{ N}.
This force acts at a distance of 0.6 meters from point C:
\text{Moment}_{4 kg} = 39.24 \text{ N} \times 0.6 \text{ m} = 23.544 \text{ Nm} (clockwise)
-
-
Moment caused by the 1.5 kg mass:
- The force due to the 1.5 kg mass is:
\text{Force} = 1.5 \text{ kg} \times 9.81 \text{ m/s}^2 \approx 14.715 \text{ N}.
This force acts at a distance of x meters from point C:
\text{Moment}_{1.5 kg} = 14.715 \text{ N} \times x \text{ m} (counterclockwise)
-
Set up the equilibrium equation:
\text{Moment}{4 kg} = \text{Moment}{1.5 kg}
This implies:
23.544 = 14.715x
-
Solve for x:
\text{x} = \frac{23.544}{14.715} \approx 1.6 ext{ m}.
Thus, the value of x is approximately 1.6 m.
