A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below. 15 (a) Use the trapezium rule with four strips to estimate the distance travelled by the particle during the time period 20 ≤ t ≤ 100. 15 (b) Over the same time period, the curve can be very closely modelled by a particular quadratic. Explain how you could find an alternative estimate using this quadratic.

A-Level AQA Maths Pure Modelling involving Numerical Methods: A particle is moving in a straig

A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below - AQA - A-Level Maths Pure - Question 15 - 2020 - Paper 2

Question 15

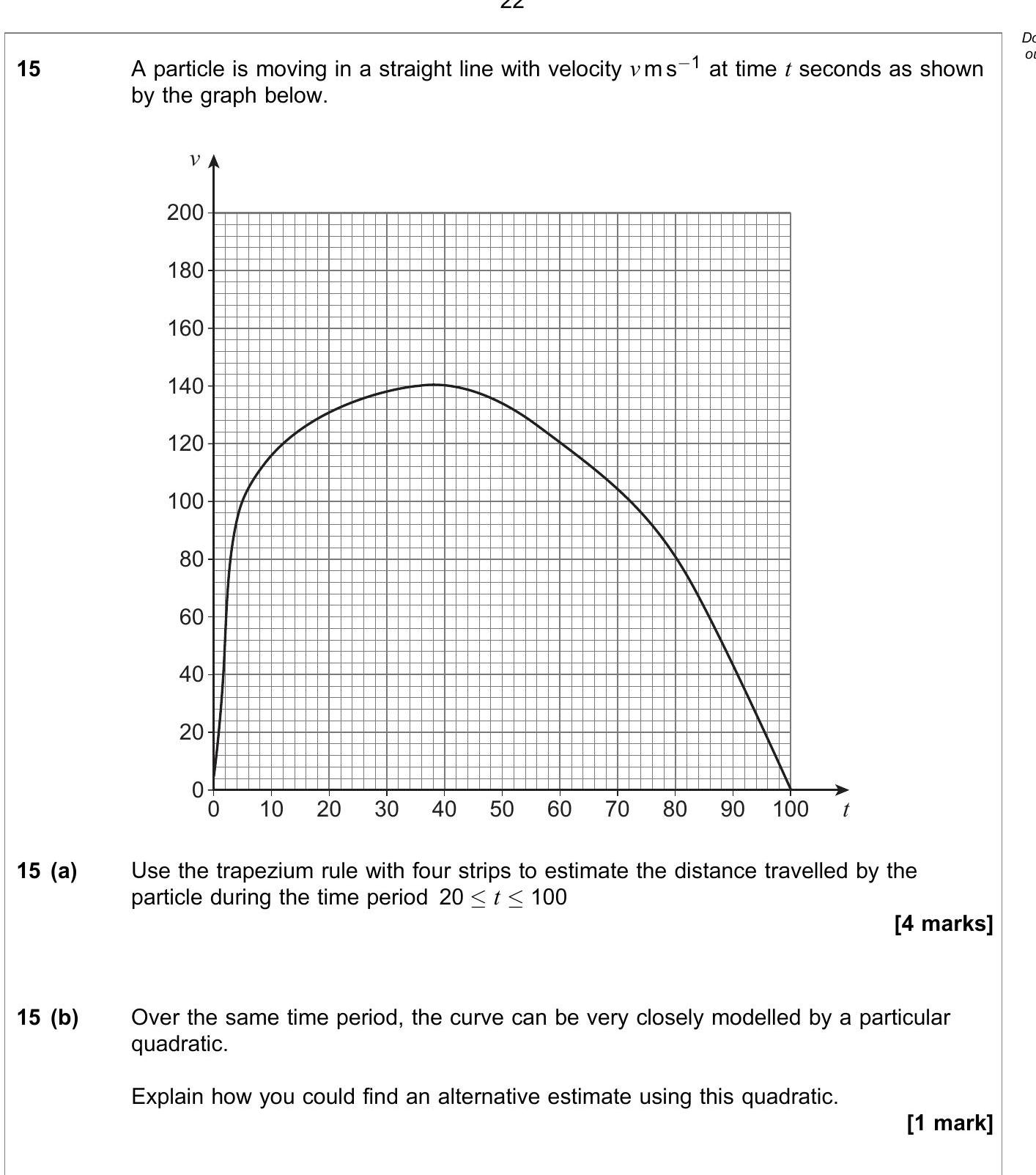
A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below. 15 (a) Use the trapezium rule with four strips to estim... show full transcript

Worked Solution & Example Answer:A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below - AQA - A-Level Maths Pure - Question 15 - 2020 - Paper 2

Step 1

Use the trapezium rule with four strips to estimate the distance travelled (15 (a))

96%

114 rated

Answer

To estimate the distance travelled using the trapezium rule, follow these steps:

Identify the relevant interval and strips: We need to use the time interval from 20 to 100 seconds. We will create four strips within this interval, which gives us an interval width of:

$h = \frac{100 - 20}{4} = 20$
Calculate the y-values at the relevant time points: From the graph, we obtain:
- At $t = 20$ , $v = 131$ m/s
- At $t = 40$ , $v = 140$ m/s
- At $t = 60$ , $v = 80$ m/s
- At $t = 80$ , $v = 67$ m/s
- At $t = 100$ , $v = 0$ m/s
Apply the trapezium rule formula: The formula for the trapezium rule is given by:

$ext{Area} = \frac{h}{2} \times (y_0 + 2y_1 + 2y_2 + 2y_3 + y_4)$

Where:
- $y_0 = 131$ , $y_1 = 140$ , $y_2 = 80$ , $y_3 = 67$ , and $y_4 = 0$ .
Substituting these values, we have:

$ext{Area} = \frac{20}{2} \times (131 + 2(140) + 2(80) + 2(67) + 0)$

$= 10 \times (131 + 280 + 160 + 134) = 10 \times 705 = 7050$
Estimate the total distance: Therefore, the estimated distance travelled by the particle during the specified period is:

$\text{Distance} = 7050 ext{ m}$

Step 2

Explain how you could find an alternative estimate using this quadratic (15 (b))

99%

104 rated

Answer

To find an alternative estimate using a quadratic to model the curve, follow these steps:

Determine the quadratic equation: After analyzing the positions of the curve from the graph, we can determine a quadratic function that accurately models the velocity of the particle over the range from 20 to 100.
Integrate the quadratic: Once the quadratic function is established, integrate it between the limits of 20 to 100.

$\text{Distance} = \int_{20}^{100} f(t) \, dt$

This approach provides a more accurate and continuous estimate of the distance travelled.
Comparison: By comparing this result with the trapezium rule estimate, we can assess the accuracy of our trapezium approximation and validate the suitability of the quadratic model.

A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below - AQA - A-Level Maths Pure - Question 15 - 2020 - Paper 2

Worked Solution & Example Answer:A particle is moving in a straight line with velocity v m s⁻¹ at time t seconds as shown by the graph below - AQA - A-Level Maths Pure - Question 15 - 2020 - Paper 2

Use the trapezium rule with four strips to estimate the distance travelled (15 (a))

Explain how you could find an alternative estimate using this quadratic (15 (b))

Join the A-Level students using SimpleStudy...