Photo AI
The graph of $y = \frac{2x^3}{x^2 + 1}$ is shown for $0 \leq x \leq 4$ Caroline is attempting to approximate the shaded area, A, under the curve using the trapezium rule by splitting the area into n trapezia - AQA - A-Level Maths Pure - Question 14 - 2019 - Paper 1
Question 14
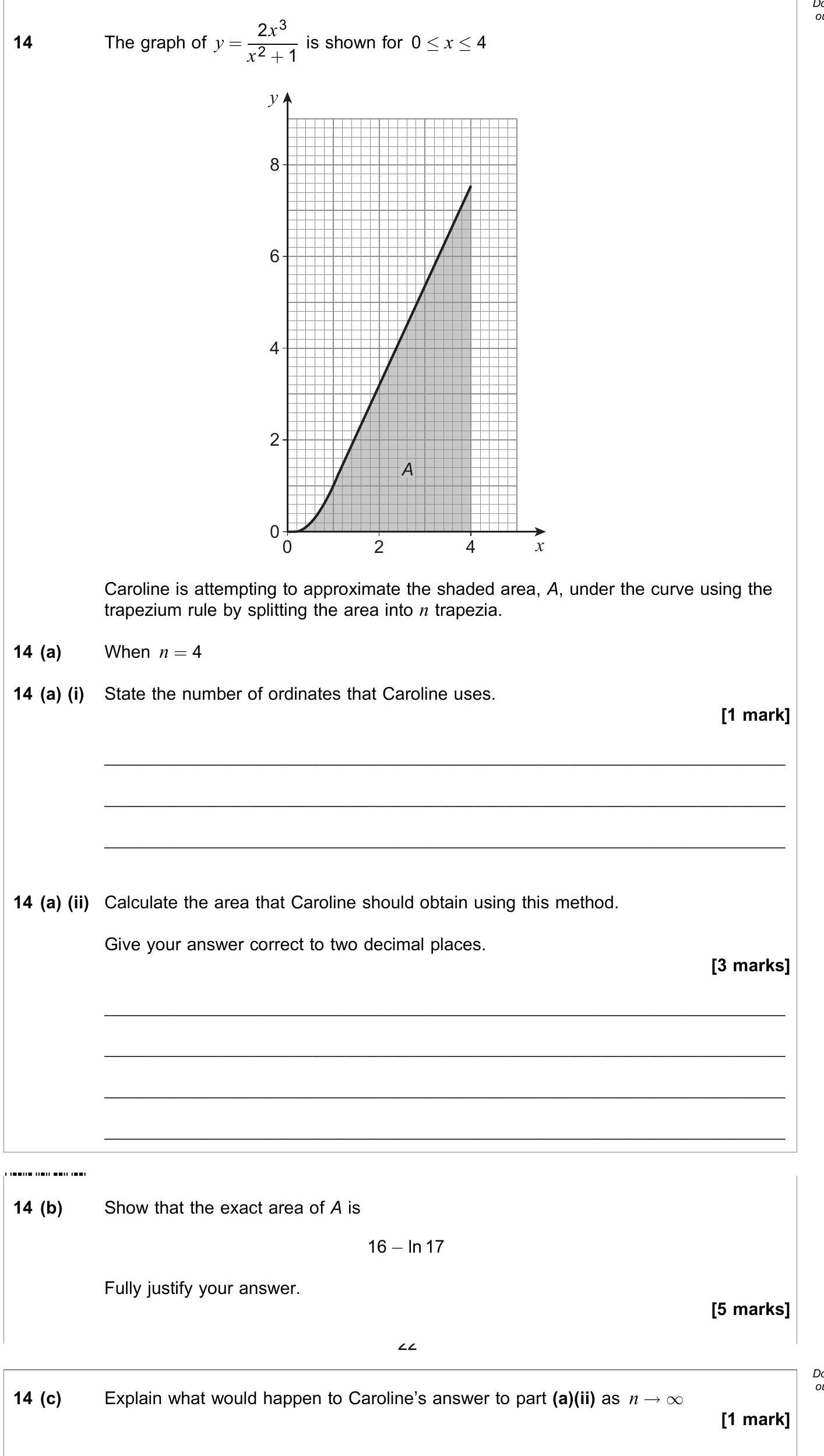
The graph of $y = \frac{2x^3}{x^2 + 1}$ is shown for $0 \leq x \leq 4$ Caroline is attempting to approximate the shaded area, A, under the curve using the trapezium... show full transcript
Worked Solution & Example Answer:The graph of $y = \frac{2x^3}{x^2 + 1}$ is shown for $0 \leq x \leq 4$ Caroline is attempting to approximate the shaded area, A, under the curve using the trapezium rule by splitting the area into n trapezia - AQA - A-Level Maths Pure - Question 14 - 2019 - Paper 1
Step 1
Step 2
Calculate the area that Caroline should obtain using this method.
Answer
To calculate the area using the trapezium rule, we first find the height at each ordinate, which occurs at , , , , and .
We calculate:
- For ,
- For ,
- For ,
- For ,
- For ,
Using the trapezium rule:
where . Thus,
Calculating this:
Thus, the area that Caroline should obtain is .
Step 3
Show that the exact area of A is $16 - \ln 17$
Answer
To find the exact area A, we integrate the function:
Using the substitution , we have , thus:
- When , .
- When , .
Rearranging for gives:
Then the integral becomes:
Calculating this:
Evaluating this from 1 to 17 results in:
Thus, confirming that the exact area A is .
Step 4
Explain what would happen to Caroline's answer to part (a)(ii) as $n \to \infty$
Answer
As , the trapezium rule becomes a more accurate approximation for the definite integral. Thus, Caroline's estimate for the area will converge towards the actual area under the curve, which we determined to be . Therefore, the error in her approximation will tend to as she increases the number of trapezia.
