Photo AI
In this question use $g = 9.8 \, \text{ms}^{-2}$\n\nA boy attempts to move a wooden crate of mass 20 kg along horizontal ground - AQA - A-Level Maths Pure - Question 13 - 2018 - Paper 2
Question 13
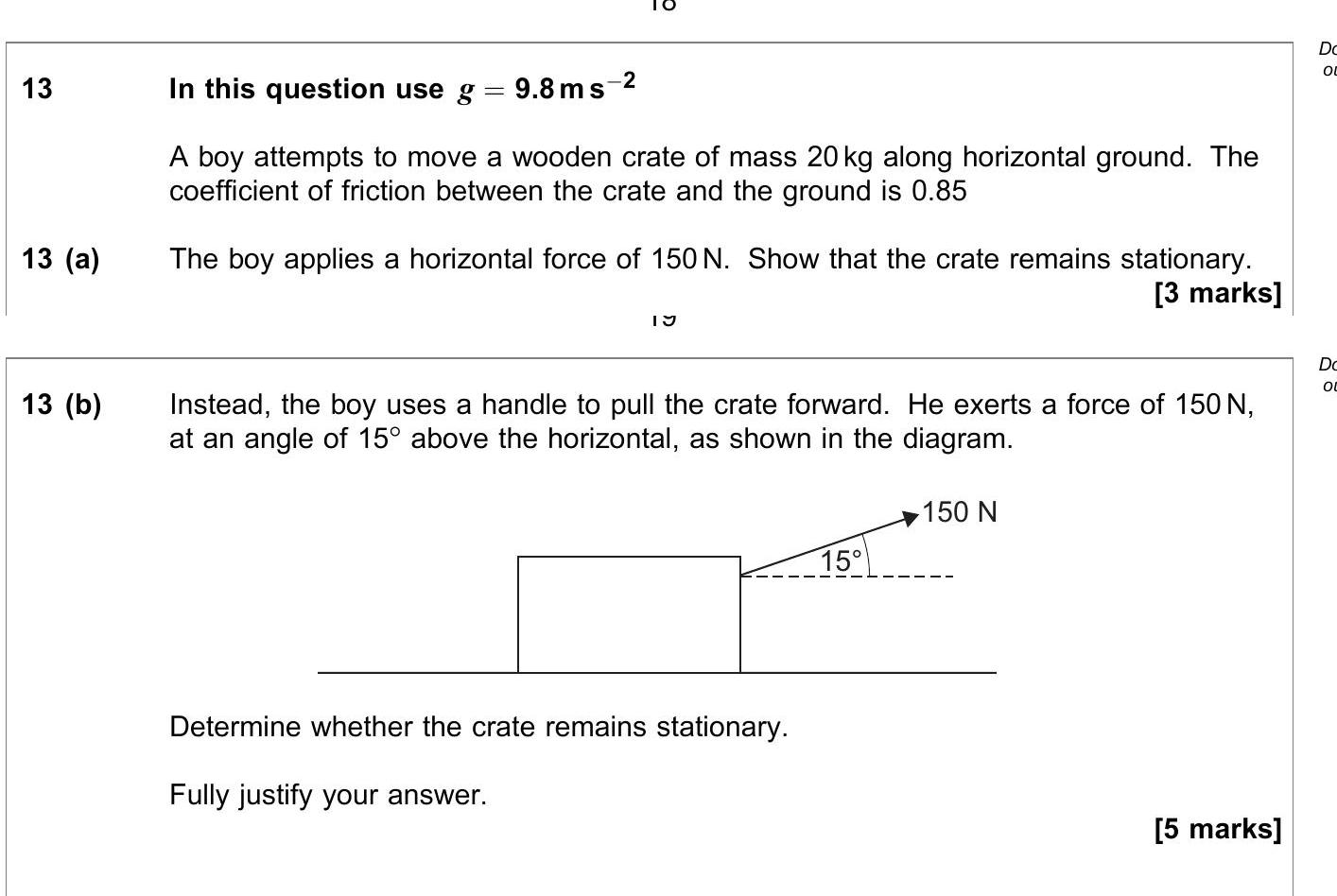
In this question use $g = 9.8 \, \text{ms}^{-2}$\n\nA boy attempts to move a wooden crate of mass 20 kg along horizontal ground. The coefficient of friction between ... show full transcript
Worked Solution & Example Answer:In this question use $g = 9.8 \, \text{ms}^{-2}$\n\nA boy attempts to move a wooden crate of mass 20 kg along horizontal ground - AQA - A-Level Maths Pure - Question 13 - 2018 - Paper 2
Step 1
13 (a) The boy applies a horizontal force of 150 N. Show that the crate remains stationary.
Answer
To determine if the crate remains stationary, we first calculate the maximum static friction force using the equation:\n\n\n\nSubstituting the given values:\n\n\n\nNow, we compare the applied force with the maximum static friction:\n\n- Applied force = 150 N\n- Maximum static friction = 166.6 N\n\nSince the applied force (150 N) is less than the maximum static friction (166.6 N), the crate does not move.
Step 2
13 (b) Instead, the boy uses a handle to pull the crate forward. He exerts a force of 150 N, at an angle of 15° above the horizontal, as shown in the diagram. Determine whether the crate remains stationary. Fully justify your answer.
Answer
In this case, we need to resolve the applied force into its horizontal and vertical components. The vertical component is given by:\n\n\n\nCalculating this gives:\n\n\n\nNext, we determine the normal force (R):\n\n\n\nSubstituting for mass and gravity:\n\n\n\nNow, we calculate the static friction force using the coefficient of friction:\n\n\n\nNext, we need the horizontal component of the applied force:\n\n\n\nFinally, we compare the horizontal force to the maximum static friction force:\n\n- Horizontal force = 144.9 N\n- Maximum static friction = 133.6 N\n\nSince the horizontal force exceeds the static friction, the crate begins to move.
