Photo AI
An object, O, of mass m kilograms is hanging from a ceiling by two light, inelastic strings of different lengths - AQA - A-Level Maths Pure - Question 18 - 2022 - Paper 2
Question 18
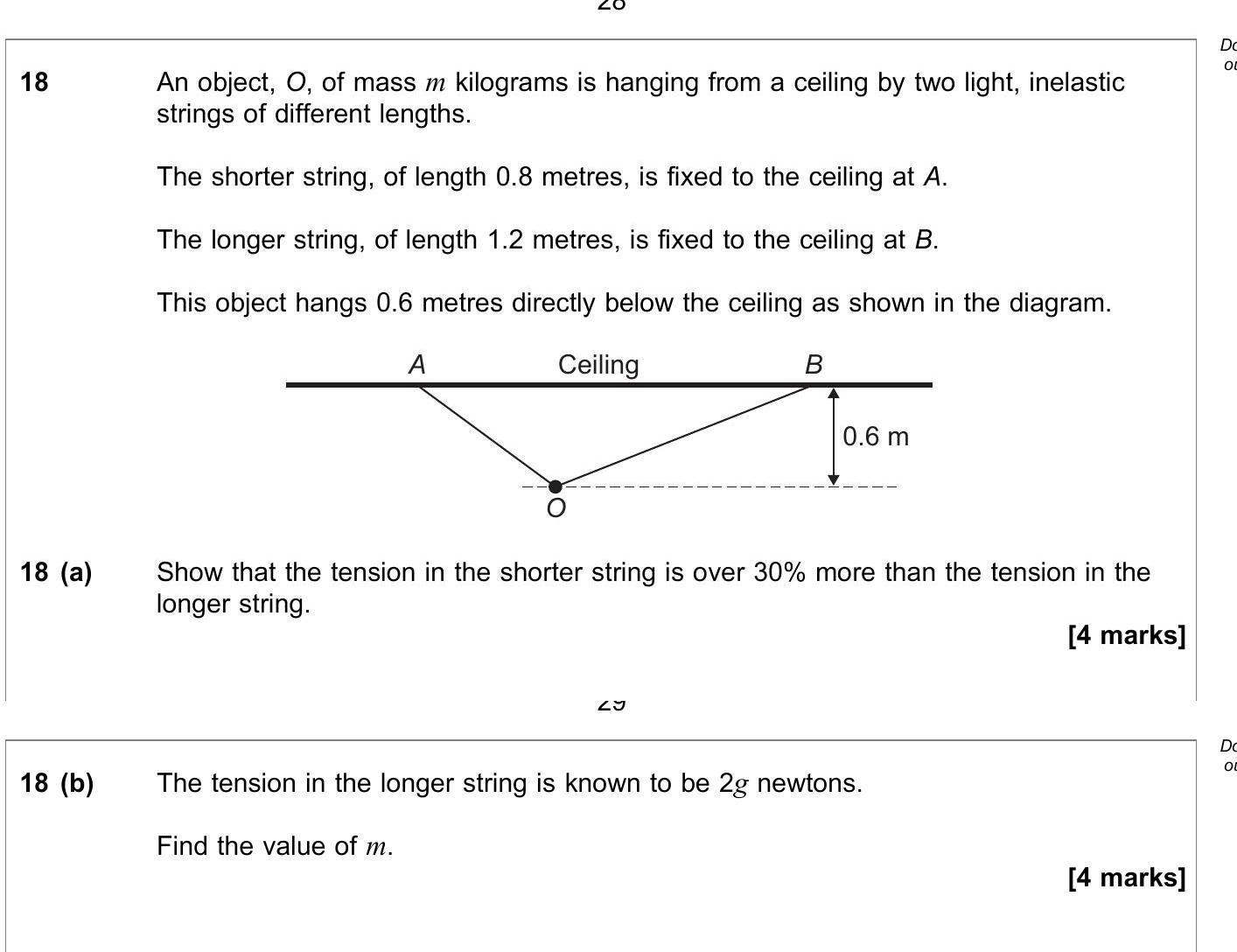
An object, O, of mass m kilograms is hanging from a ceiling by two light, inelastic strings of different lengths. The shorter string, of length 0.8 metres, is fixed... show full transcript
Worked Solution & Example Answer:An object, O, of mass m kilograms is hanging from a ceiling by two light, inelastic strings of different lengths - AQA - A-Level Maths Pure - Question 18 - 2022 - Paper 2
Step 1
Show that the tension in the shorter string is over 30% more than the tension in the longer string.
Answer
To demonstrate that the tension in the shorter string is more than 30% greater than that in the longer string, we start by applying the sine rule and geometry.
The angles for the strings are derived using trigonometry. Let:
- Angle at A,
- Angle at B,
Using equilibrium conditions, we can set up the horizontal component equations:
Thus,
Substituting the angles:
Calculating:
Therefore:
This indicates that:
Since 1.3 is greater than 1.3, we conclude that the tension in the shorter string on average is more than 30% more than that in the longer string.
Step 2
The tension in the longer string is known to be 2g newtons. Find the value of m.
Answer
In this part, we analyze the forces in the vertical direction. The forces acting on the object include the weight and tension of the strings:
Let the tension in the longer string be:
From our earlier equation:
Substituting the values:
So:
We earlier found:
So substituting: Solving gives:
Thus, the value of m is 3.0 kilograms.
