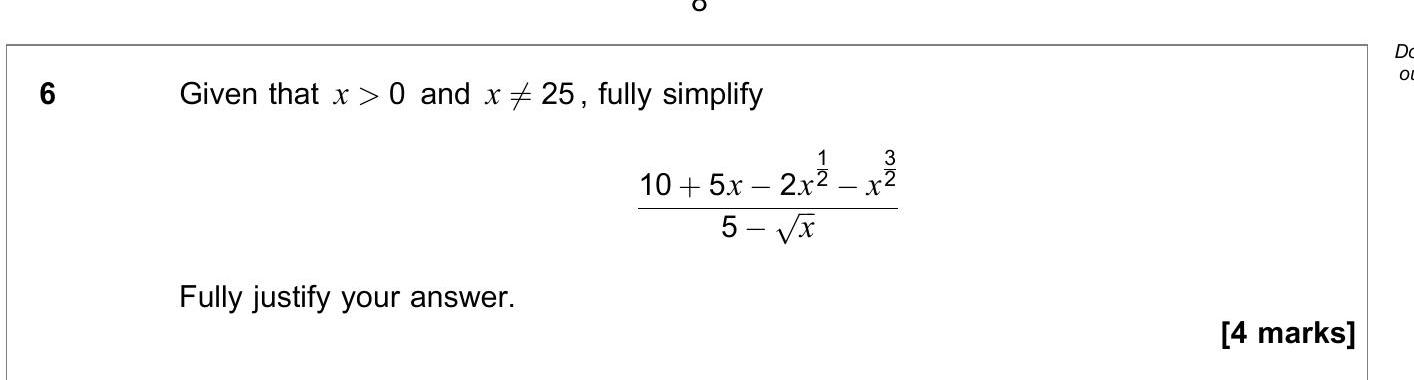Given that $x > 0$ and $x \neq 25$, fully simplify
$$\frac{10 + 5x - 2x^{\frac{3}{2}} - x^2}{5 - \sqrt{x}}$$
Fully justify your answer. - AQA - A-Level Maths Pure - Question 6 - 2021 - Paper 3

Question 6
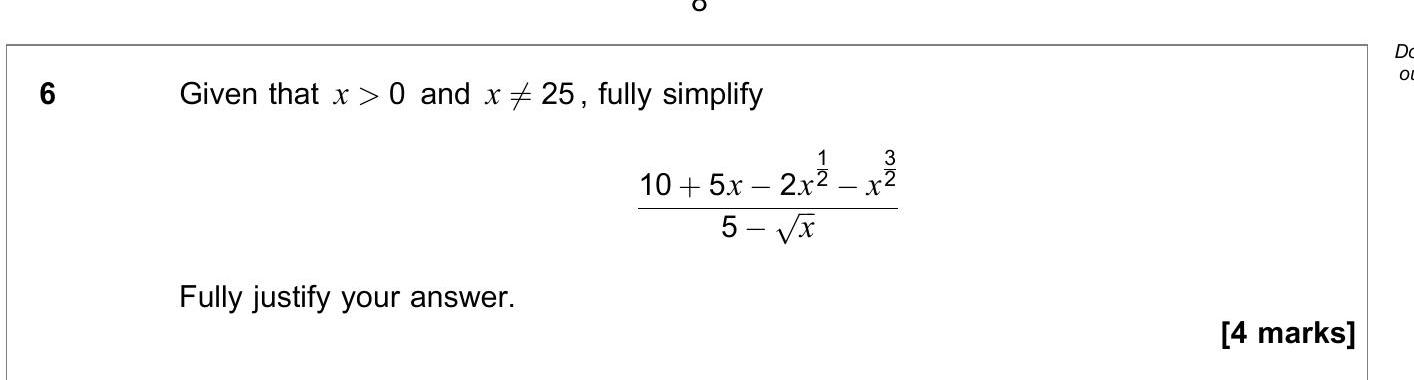
Given that $x > 0$ and $x \neq 25$, fully simplify
$$\frac{10 + 5x - 2x^{\frac{3}{2}} - x^2}{5 - \sqrt{x}}$$
Fully justify your answer.
Worked Solution & Example Answer:Given that $x > 0$ and $x \neq 25$, fully simplify
$$\frac{10 + 5x - 2x^{\frac{3}{2}} - x^2}{5 - \sqrt{x}}$$
Fully justify your answer. - AQA - A-Level Maths Pure - Question 6 - 2021 - Paper 3
Write the expression for simplification

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We begin with the expression:
5−x10+5x−2x23−x2
Factor the numerator

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To simplify the numerator, we can rewrite it as:
10+5x−(2x23+x2)
Recognizing that x2=x2, we factor:
10+5x−(x2(2x+1))
Identify a common factor

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We notice that the terms have a common factor of x in the quadratic expression:
⇒10+5x−x(2x+1)
Thus, we can group:
=(10+5x)−x(2x+1)
Cancel the common factor

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
The expression can now be simplified further by cancelling the common factor of (5−x):
(5−x)(10+5x)
Thus, our expression simplifies to:
2+x
Join the A-Level students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered