A-Level AQA Maths Pure Graphs of Functions: Identify the graph of $y = 1

Identify the graph of $y = 1 - |x + 2|$ from the options below - AQA - A-Level Maths Pure - Question 1 - 2019 - Paper 2

Question 1

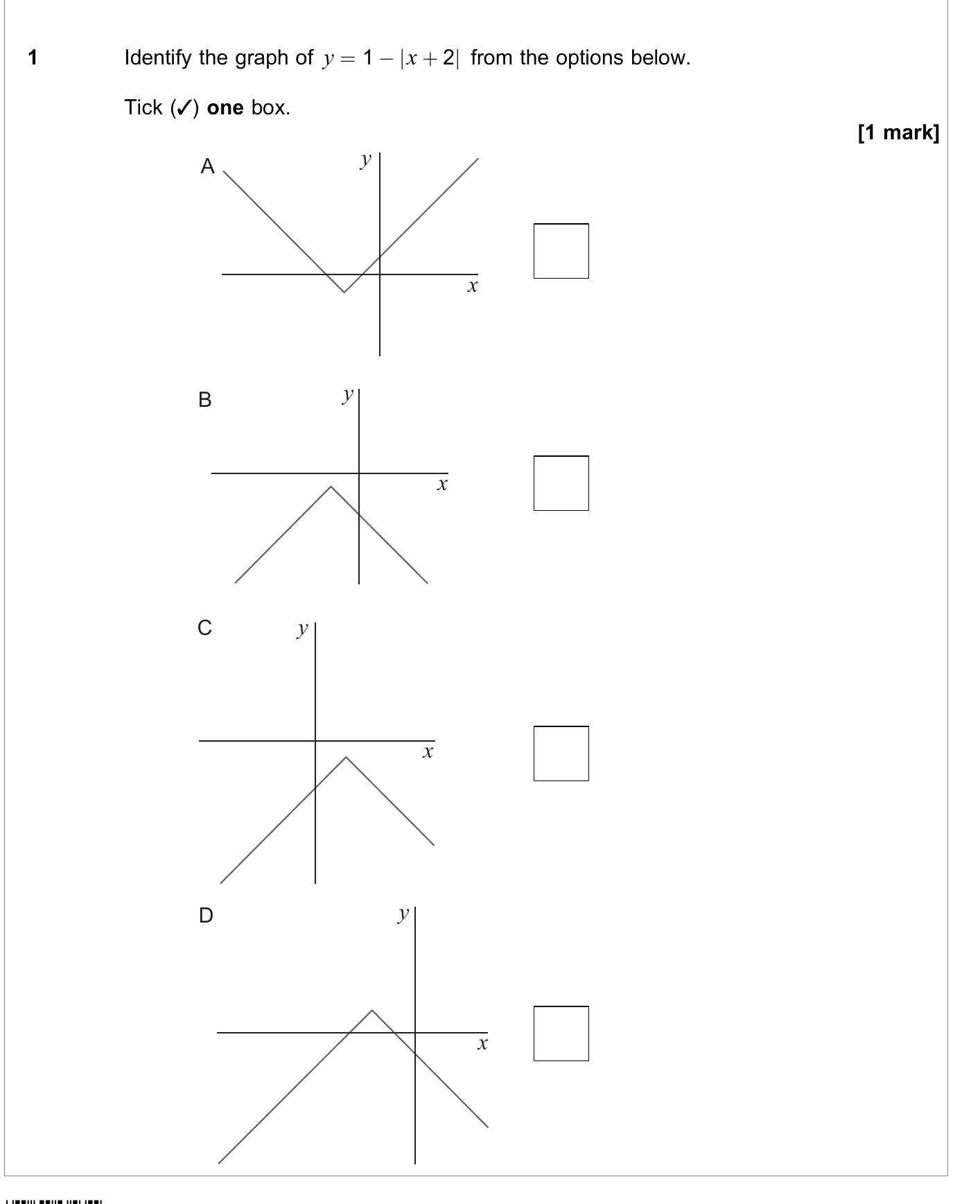
Identify the graph of $y = 1 - |x + 2|$ from the options below. Tick (✓) one box. A B C D

Worked Solution & Example Answer:Identify the graph of $y = 1 - |x + 2|$ from the options below - AQA - A-Level Maths Pure - Question 1 - 2019 - Paper 2

Step 1

96%

114 rated

Answer

To identify the graph of the function $y = 1 - |x + 2|$ , we need to analyze its characteristics:

Vertex: The absolute value function $|x + 2|$ has its vertex at $x = -2$ . Therefore, the vertex of the graph of $y = 1 - |x + 2|$ is at the point $(-2, 1)$ .
Shape: The graph will be a V-shape, opening downwards, due to the negative sign in front of the absolute value.
Intercepts:
- Y-intercept: Set $x = 0$ :
  $y = 1 - |0 + 2| = 1 - 2 = -1.$
  So, the y-intercept is at (0, -1).
- X-intercepts: Set $y = 0$ $y = 0$ :
  $0 = 1 - |x + 2| \Rightarrow |x + 2| = 1.$ $0 = 1 - ∣ x + 2∣ \Rightarrow ∣ x + 2∣ = 1.$
  Solving this gives:
  - $x + 2 = 1 \Rightarrow x = -1$
  - $x + 2 = -1 \Rightarrow x = -3$
    Therefore, the x-intercepts are at (-1, 0) and (-3, 0).
Plotting Points:
- Vertex at (-2, 1)
- Y-intercept at (0, -1)
- X-intercepts at (-1, 0) and (-3, 0)

Looking carefully at the given options, the correct graph that depicts these intercepts and the overall downward opening V-shape is D.