Photo AI
Show that the exact value of sin θ is \( \frac{\sqrt{4}}{15} \). - AQA - A-Level Maths Pure - Question 2 - 2019 - Paper 3
Question 2
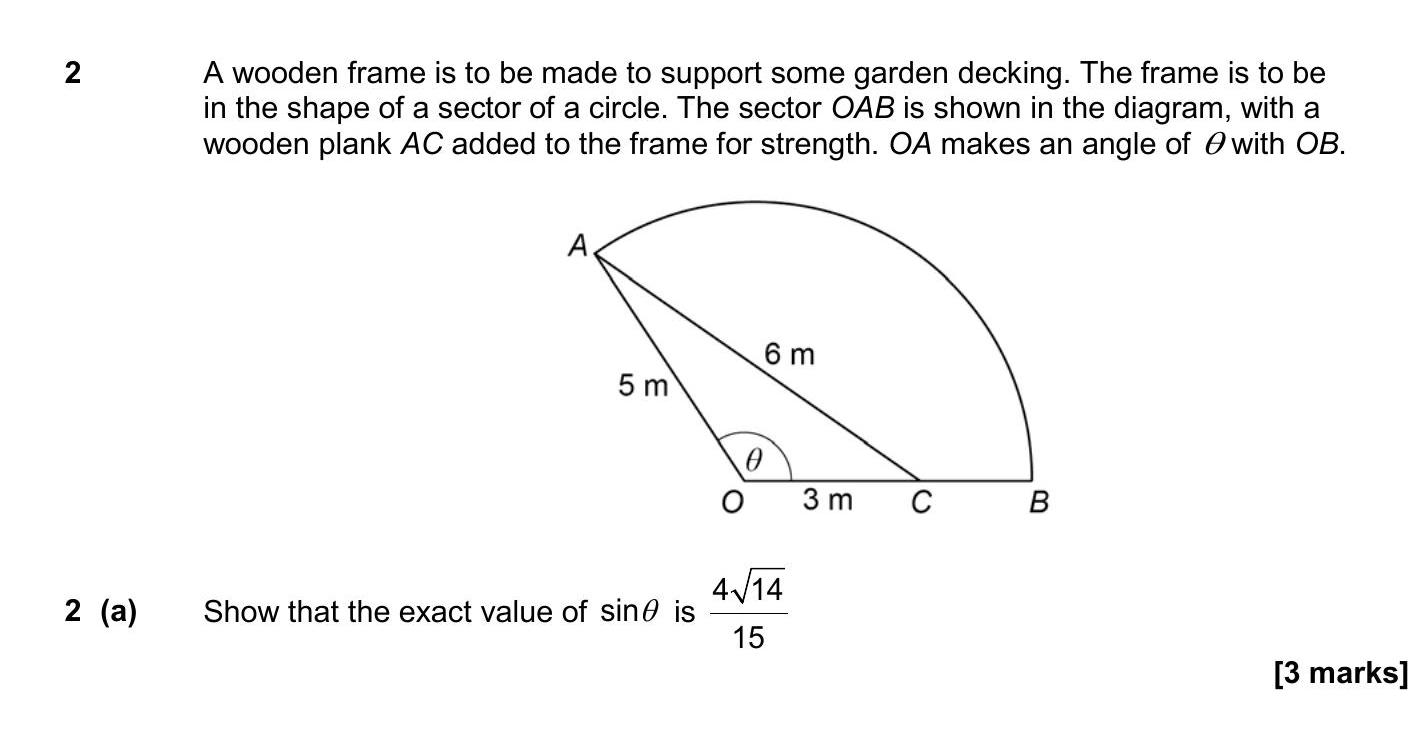
Show that the exact value of sin θ is \( \frac{\sqrt{4}}{15} \).
Worked Solution & Example Answer:Show that the exact value of sin θ is \( \frac{\sqrt{4}}{15} \). - AQA - A-Level Maths Pure - Question 2 - 2019 - Paper 3
Step 1
Step 2
Step 3
