Photo AI
A particle’s displacement, r metres, with respect to time, t seconds, is defined by the equation $r = 3e^{0.5t}$ Find an expression for the velocity, v m s$^{-1}$, of the particle at time t seconds - AQA - A-Level Maths Pure - Question 11 - 2021 - Paper 2
Question 11
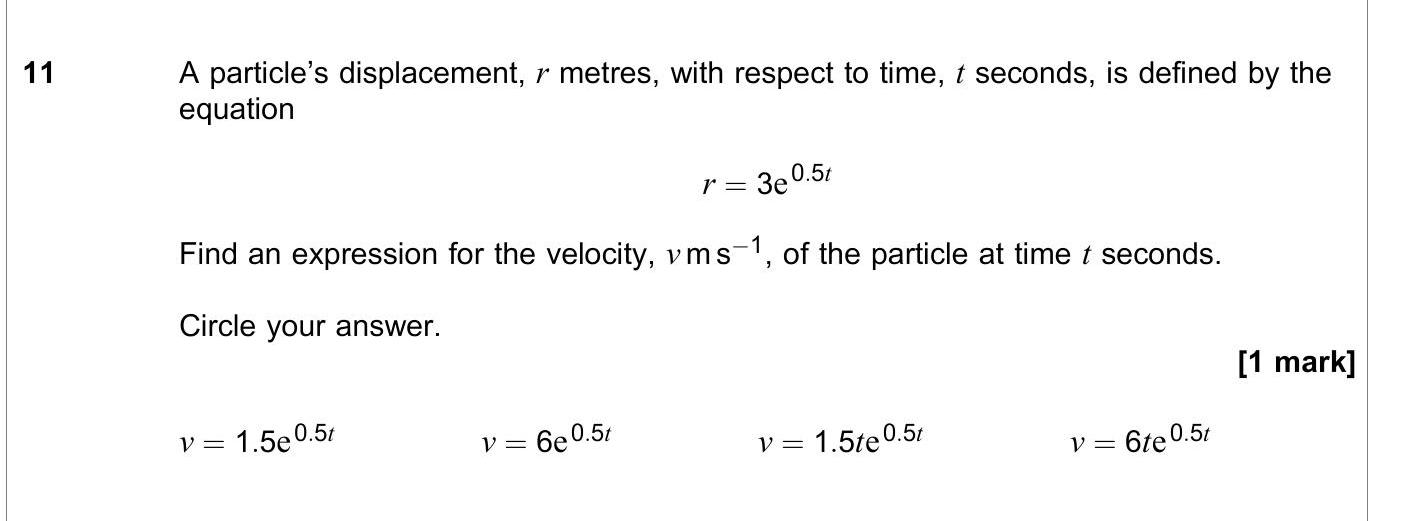
A particle’s displacement, r metres, with respect to time, t seconds, is defined by the equation $r = 3e^{0.5t}$ Find an expression for the velocity, v m s$^{-1}$,... show full transcript
Worked Solution & Example Answer:A particle’s displacement, r metres, with respect to time, t seconds, is defined by the equation $r = 3e^{0.5t}$ Find an expression for the velocity, v m s$^{-1}$, of the particle at time t seconds - AQA - A-Level Maths Pure - Question 11 - 2021 - Paper 2
Step 1
Find an expression for the velocity, v m s$^{-1}$
Answer
To find the velocity of the particle, we need to take the derivative of the displacement function with respect to time.
Given the displacement:
we calculate the velocity as follows:
Using the chain rule, we get:
The derivative of is , where :
Thus, substituting back, we have:
Therefore, the expression for the velocity of the particle at time t seconds is:
This is the correct answer.
