A cylinder is to be cut out of the circular face of a solid hemisphere. The cylinder and the hemisphere have the same axis of symmetry. The cylinder has height $h$ and the hemisphere has a radius of $R$. 9 (a) Show that the volume, $V$, of the cylinder is given by $$V = u R^2 h - rac{\pi h^3}{3}$$ 9 (b) Find the maximum volume of the cylinder in terms of $R$. Fully justify your answer.

A-Level AQA Maths Pure Applications of Differentiation: A cylinder is to be cut out of t

A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2

Question 9

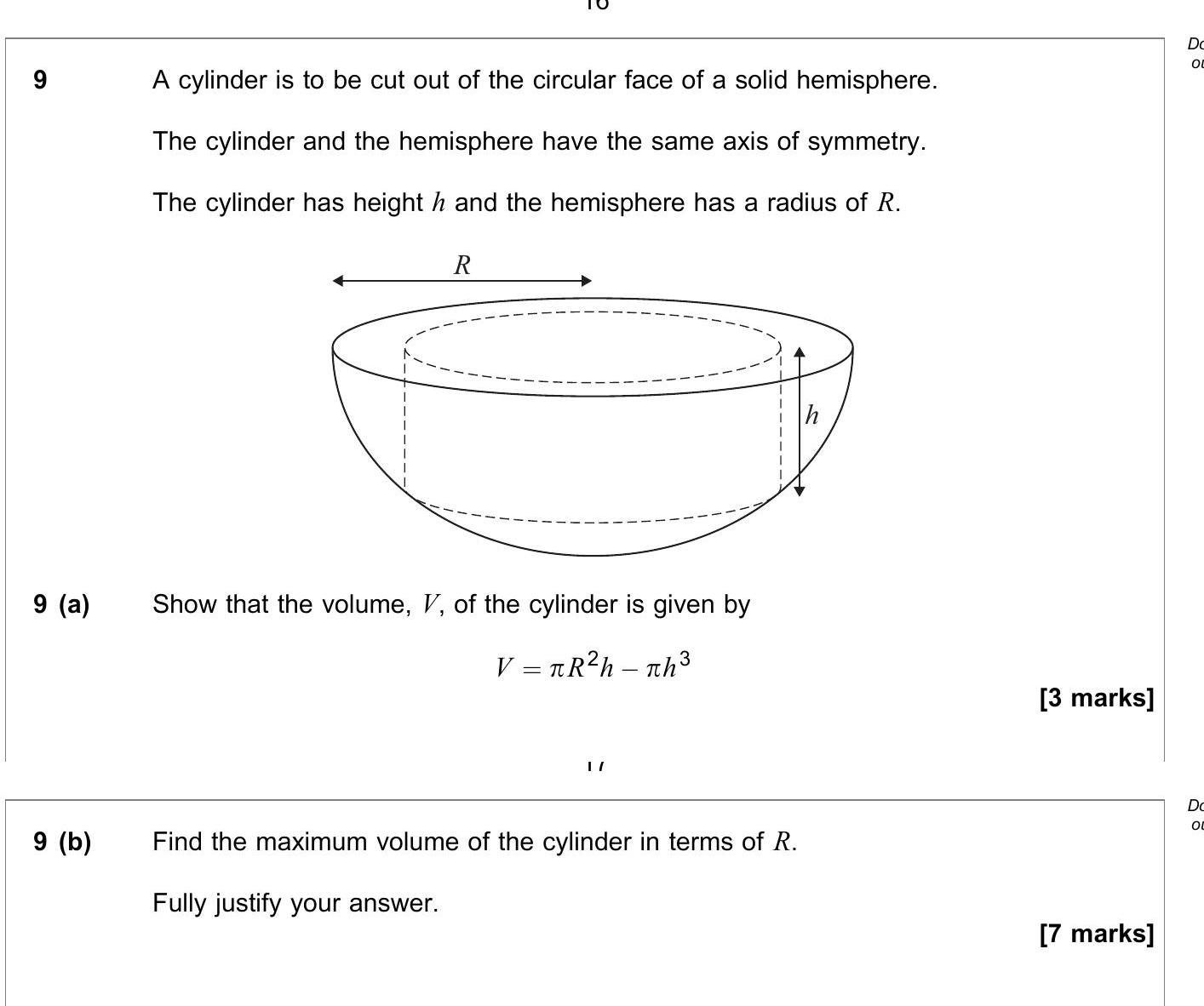
A cylinder is to be cut out of the circular face of a solid hemisphere. The cylinder and the hemisphere have the same axis of symmetry. The cylinder has height $h$ a... show full transcript

Worked Solution & Example Answer:A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2

Step 1

Show that the volume, $V$, of the cylinder is given by

96%

114 rated

Answer

To derive the volume of the cylinder, we begin with the formula for the volume of a cylinder, which is given by:

$V = ext{Base Area} \times ext{Height} = \pi r^2 h$

Here, $r$ is the radius of the cylinder. Since the base of the cylinder is inscribed in the hemisphere, we can use the Pythagorean theorem to relate $r$ , $h$ , and $R$ :

$r^2 + h^2 = R^2 o r = \sqrt{R^2 - h^2}$

Now substituting $r$ back into the volume formula:

$V = \pi (R^2 - h^2) h$

Expanding this gives:

$V = \pi R^2 h - \pi h^3$

Thus, we have shown that:

$V = \pi R^2 h - \frac{\pi h^3}{3}$

Step 2

Find the maximum volume of the cylinder in terms of $R$. Fully justify your answer.

99%

104 rated

Answer

To find the maximum volume, we need to differentiate the volume function $V$ with respect to $h$ and set the derivative equal to zero:

First, we differentiate:

$\frac{dV}{dh} = \pi R^2 - 3\pi h^2$

Setting this equal to zero for maximum volume:

$\pi R^2 - 3\pi h^2 = 0$

Thus,

$3\pi h^2 = \pi R^2 \Rightarrow h^2 = \frac{R^2}{3} \Rightarrow h = \frac{R}{\sqrt{3}}$

Now, substituting $h$ back into the volume equation to find the maximum volume:

$V = \pi R^2 \left(\frac{R}{\sqrt{3}}\right) - \frac{\pi}{3} \left(\frac{R}{\sqrt{3}}\right)^3$

This simplifies to:

$V = \frac{\pi R^3}{\sqrt{3}} - \frac{\pi R^3}{9\sqrt{3}} = \frac{2\pi R^3}{3\sqrt{3}}$

We also check the second derivative to confirm that this is indeed a maximum:

$\frac{d^2V}{dh^2} = -6\pi h$

Since $h > 0$ , we have:

$\frac{d^2V}{dh^2} < 0$

This indicates that the volume has a maximum at this $h$ value.

A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2

Worked Solution & Example Answer:A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2

Show that the volume, $V$, of the cylinder is given by

Find the maximum volume of the cylinder in terms of $R$. Fully justify your answer.

Join the A-Level students using SimpleStudy...