Photo AI
A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2
Question 9
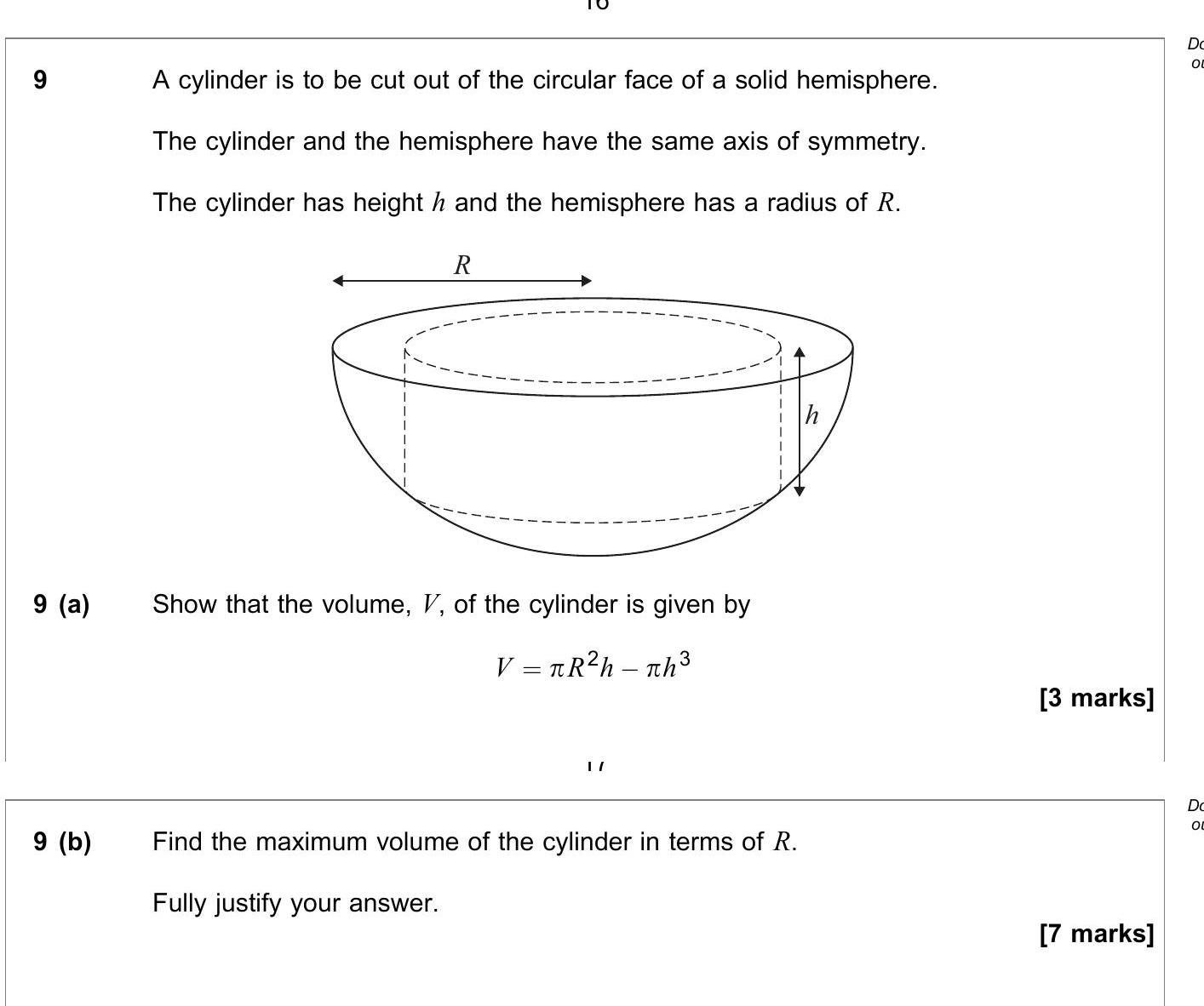
A cylinder is to be cut out of the circular face of a solid hemisphere. The cylinder and the hemisphere have the same axis of symmetry. The cylinder has height $h$ a... show full transcript
Worked Solution & Example Answer:A cylinder is to be cut out of the circular face of a solid hemisphere - AQA - A-Level Maths Pure - Question 9 - 2020 - Paper 2
Step 1
Show that the volume, V, of the cylinder is given by
Answer
To find the volume of the cylinder, we first identify the relevant variables. The volume of a cylinder can be expressed as:
The base area of the cylinder is a circle with radius . Therefore:
V = ext{Area of Base} imes h = ext{Area of } imes h = ext{Base Area} = au imes r^{2} imes h = au imes R^{2} - rac{ heta}{3}.
Next, we need to express in terms of . Using the geometry of the situation:
From the right triangle formed, we apply the Pythagorean theorem:
Thus, we can derive as:
Substituting into the volume formula yields:
V = au imes (R^{2} - h^{2}) imes h = au R^{2}h - rac{ heta}{3},
which completes the proof.
Step 2
Find the maximum volume of the cylinder in terms of R.
Answer
To find the maximum volume of the cylinder, we first take the derived volume formula:
V = au R^{2}h - rac{ heta}{3}
Next, we differentiate the volume with respect to height :
Setting this equal to zero to find critical points for maximum volume:
This implies:
Next, we also need to consider the values of . The maximum occurs either when or , but we focus on the stationary points:
Substituting this back into the volume expression:
We arrive at the form:
V = K R^{2} h - rac{ heta}{3}
Hence, substituting the term in the formula:
Finally, to verify the maximum, substitute back into the differentiative volume formula:
showing that this indeed provides a maximum volume.
