Photo AI
Given the function y = e^{-x} ( sin x + cos x ) Find $\frac{dy}{dx}$ - AQA - A-Level Maths Pure - Question 16 - 2019 - Paper 1
Question 16
Given the function y = e^{-x} ( sin x + cos x ) Find $\frac{dy}{dx}$. Simplify your answer. Hence, show that $\int e^{-x} sin x \: dx = -a e^{-x} ( sin x + cos... show full transcript
Worked Solution & Example Answer:Given the function y = e^{-x} ( sin x + cos x ) Find $\frac{dy}{dx}$ - AQA - A-Level Maths Pure - Question 16 - 2019 - Paper 1
Step 1
Find $\frac{dy}{dx}$
Answer
To differentiate the function, we employ the product rule:
- Let and .
- Then, [\frac{dy}{dx} = u'v + uv']
- Computing the derivatives:
- Substitute these into the product rule: [\frac{dy}{dx} = (-e^{-x})(sin x + cos x) + e^{-x}(cos x - sin x)]
- Simplifying the expression gives: [\frac{dy}{dx} = -e^{-x}(sin x + cos x) + e^{-x}(cos x - sin x)] [= e^{-x}(-sin x - cos x + cos x - sin x) = -2e^{-x} sin x]
Step 2
Show that $\int e^{-x} sin x \: dx = -a e^{-x} ( sin x + cos x) + c$ where $a$ is a rational number.
Answer
To solve the integral, we use integration by parts:
- Let and . Thus, and .
- Applying integration by parts yields: [\int e^{-x} sin x : dx = -e^{-x} sin x - \int -e^{-x} cos x : dx]
- This implies: [\int e^{-x} sin x : dx = -e^{-x} sin x + \int e^{-x} cos x : dx]
- Similarly, integrating (using parts again), we get: [\int e^{-x} cos x : dx = -e^{-x} cos x + \int e^{-x} sin x : dx]
- Combining these results gives:
- Solving for the integral leads to the conclusion that the constant .
Step 3
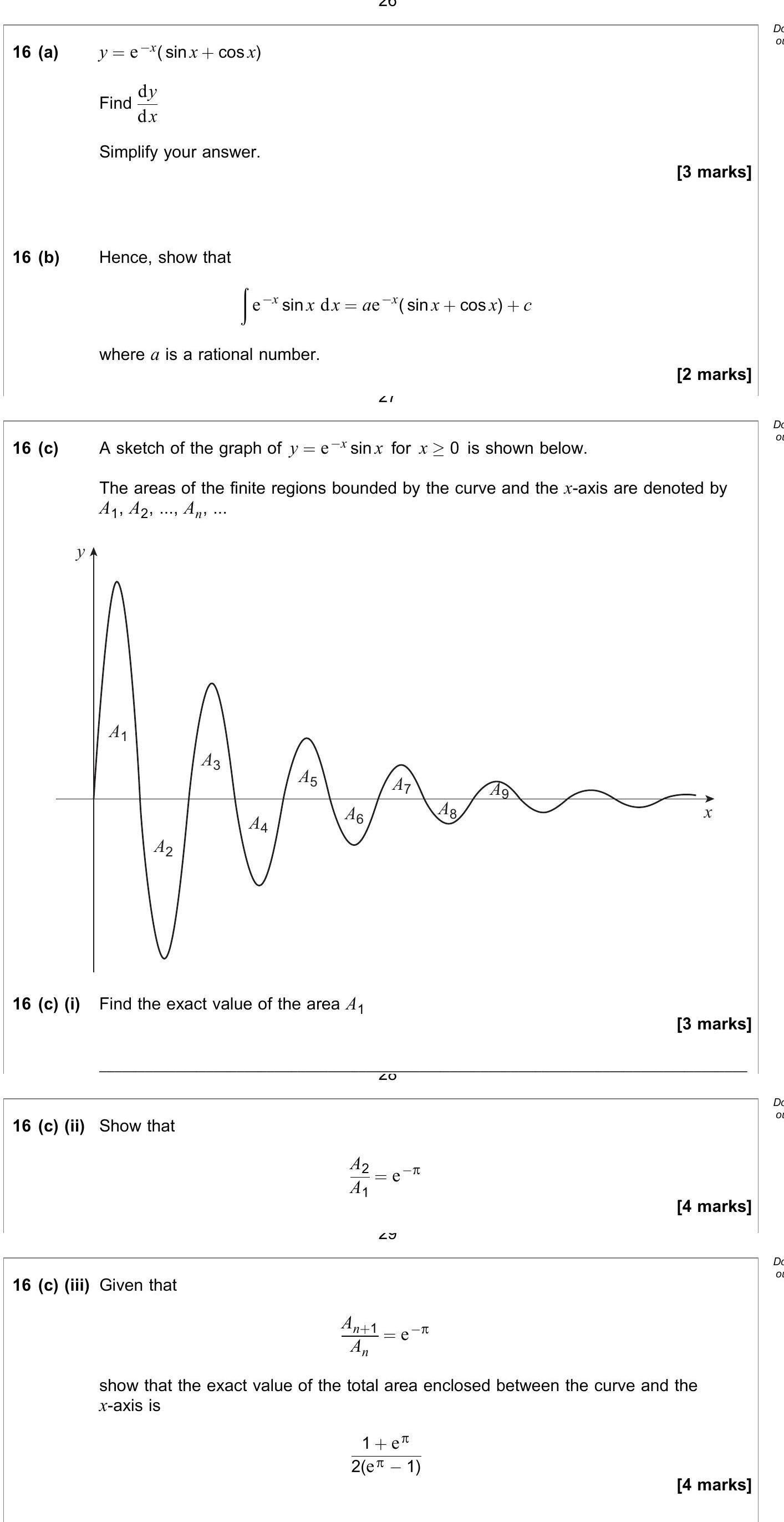
Find the exact value of the area $A_1$
Answer
To find the area , we calculate:
- The area can be expressed as: [A_1 = \int_0^{\pi} e^{-x} sin x : dx]
- Using the result from part (b), we have: [A_1 = -e^{-\pi}(sin(\pi) + cos(\pi)) + e^{0}(sin(0) + cos(0))]
- This simplifies to: [A_1 = -e^{-\pi}(0 - 1) + 1(0 + 1) = e^{-\pi} + 1 = \frac{1 + e^{-\pi}}{2}]
Step 4
Step 5
Show that the exact value of the total area enclosed between the curve and the x-axis is $\frac{1 + e^{-\pi}}{2( e - 1 )}$
Answer
To find the total area, we express the series:
- Knowing the ratio suggests a geometric series.
- The total area can be evaluated as: [\text{Total Area} = A_1 \frac{1}{1 - r},] where .
- This leads us to: [\text{Total Area} = A_1 \frac{1}{1 - e^{-\pi}}]
- Substitute $A_1 = \frac{1 + e^{-\pi}}{2}] and simplify to achieve the final form.
