Photo AI
16 (a) y = e^{-x} (sin x + cos x) Find \( \frac{dy}{dx} \) Simplify your answer - AQA - A-Level Maths Pure - Question 16 - 2019 - Paper 1
Question 16
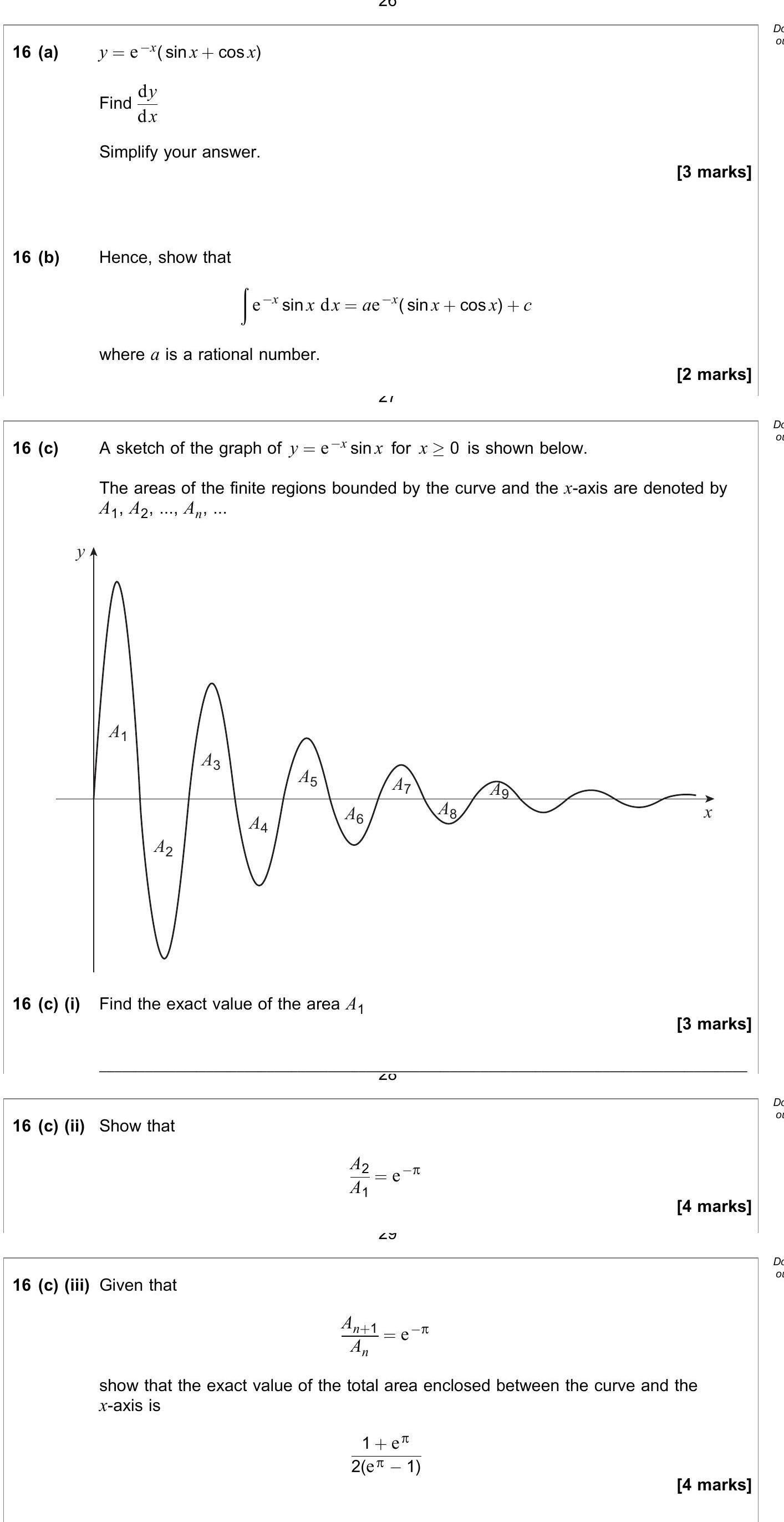
16 (a) y = e^{-x} (sin x + cos x) Find \( \frac{dy}{dx} \) Simplify your answer. (3 marks) 16 (b) Hence, show that \( \int e^{-x} sin x dx = a e^{-x} (sin... show full transcript
Worked Solution & Example Answer:16 (a) y = e^{-x} (sin x + cos x) Find \( \frac{dy}{dx} \) Simplify your answer - AQA - A-Level Maths Pure - Question 16 - 2019 - Paper 1
Step 1
Find \( \frac{dy}{dx} \)
Answer
To find ( \frac{dy}{dx} ), we will use the product rule. Let ( u = e^{-x} ) and ( v = sin x + cos x ). Then, the product rule states that:
[ \frac{d(uv)}{dx} = u'v + uv' ]
Calculating each component: [ u' = rac{d}{dx}(sin x + cos x) = cos x - sin x ] [ u' = -e^{-x} ]
Substituting back, we get: [ \frac{dy}{dx} = e^{-x}(cos x + cos x) + (sin x + cos x)(-e^{-x}) = e^{-x}(2cos x - (sin x + cos x)) ]
Simplifying this, we have:
[ \frac{dy}{dx} = e^{-x}(-sin x + cos x) ]
Step 2
Hence, show that \(\int e^{-x} sin x dx = a e^{-x} (sin x + cos x) + c\)
Answer
To show this, we can apply integration by parts. Let ( u = sin x ) and ( dv = e^{-x}dx ). Therefore, we have:
[ \int e^{-x} sin x dx = -e^{-x} (sin x - cos x) + \int e^{-x} cos x dx ]
By applying integration by parts again, we find: [ \int e^{-x} cos x dx = e^{-x} (cos x + sin x) + c ]
Thus, combining these results, we can express: [ \int e^{-x} sin x dx = a e^{-x} (sin x + cos x) + c ] for some rational number ( a ).
Step 3
Step 4
Step 5
Show that the exact value of the total area enclosed is \( \frac{1 + e^{-\pi}}{2(e - 1)} \)
Answer
Using the geometric series based on the ratio: [ \sum_{n=0}^{\infty} A_1 (e^{-\pi})^n ]
This converges to: [ \frac{A_1}{1 - e^{-\pi}} = \frac{e^{-\pi} - 1}{2(e - 1)} ]
Collectively yielding: [ \frac{1 + e^{-\pi}}{2(e - 1)} ] for the total area.
