Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. | $v / 10^8 \, m \, s^{-1}$ | $E_k \, MeV$ | |----------------------------|----------------| | 2.60 | 0.5 | | 2.73 | 0.7 | | 2.88 | 1.3 | | 2.96 | 2.6 | | 2.99 | 5.8 | 0 4 1 Classical mechanics predicts that $E_k \propto v^2$. Deduce whether the data in Table 1 are consistent with this prediction. 0 4 2 Discuss how Einstein's theory of special relativity explains the data in Table 1. 0 4 3 Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Photo AI

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Question 4

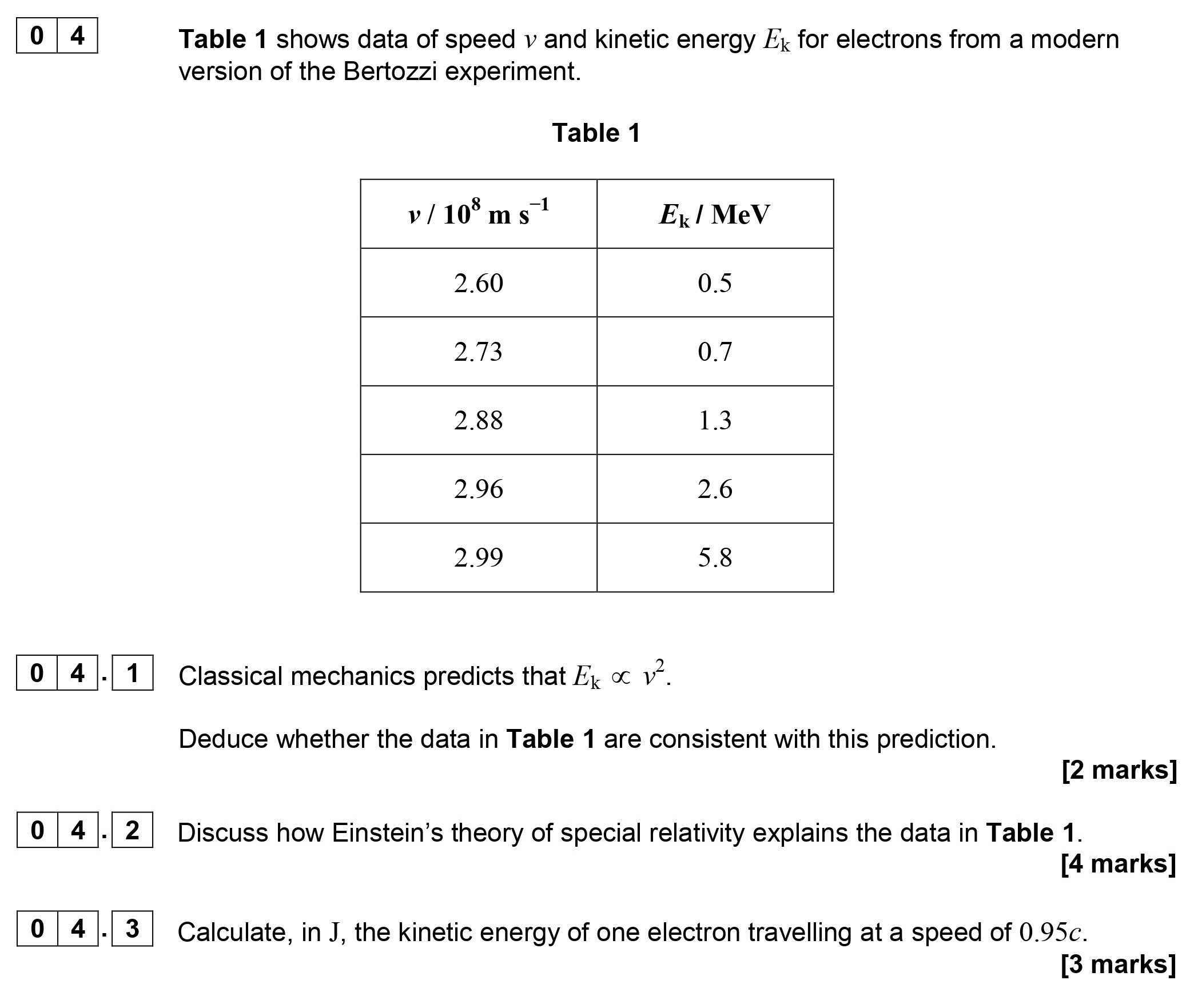
Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. | $v / 10^8 \, m \, s^{-1}$ | $E_k \, MeV$ ... show full transcript

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Step 1

Deduce whether the data in Table 1 are consistent with this prediction.

96%

114 rated

Answer

To determine if the data are consistent with $E_k \propto v^2$ , we will check if the kinetic energy increases proportionally with the square of the speed.

Taking some data pairs from Table 1:
- For $v = 2.60 \times 10^8 \, m \, s^{-1}$ , $E_k = 0.5 \, MeV$ . If we express $E_k$ in Joules, we convert MeV to Joules: 1 MeV $= 1.6 \times 10^{-13} \, J$ , thus:
$E_k = 0.5 imes 1.6 \times 10^{-13} = 8.0 \times 10^{-14} \, J$
- For $v = 2.73 \times 10^8 \, m \, s^{-1}$ , $E_k = 0.7 \, MeV$ :
$E_k = 0.7 \times 1.6 \times 10^{-13} = 1.12 \times 10^{-13} \, J$
- For $v = 2.88 \times 10^8 \, m \, s^{-1}$ , $E_k = 1.3 \, MeV$ :
$E_k = 1.3 \times 1.6 \times 10^{-13} = 2.08 \times 10^{-13} \, J$
- Calculating the ratio of $E_k$ to $v^2$ for these points can confirm the proportionality. If all ratios are constant, the data are consistent with the prediction.

Step 2

Discuss how Einstein's theory of special relativity explains the data in Table 1.

99%

104 rated

Answer

Einstein's theory of special relativity modifies the classical kinetic energy equation, especially at speeds close to the speed of light (c). The kinetic energy is given by:

$E_k = \left(\frac{mv}{\sqrt{1 - \frac{v^2}{c^2}}} - m \right) c^2$

Where $m$ is the rest mass and $v$ is the velocity. As $v$ approaches $c$ , the denominator approaches zero, which results in a significant increase in kinetic energy. Thus, the data from Table 1 indicates that as the speed of the electrons increases (approaching the speed of light), the increase in kinetic energy is greater than predicted by classical mechanics, supporting Einstein's theory that mass increases with speed. The data clearly shows a nonlinear relationship that aligns with the relativistic model, especially where speeds are higher.

Step 3

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

96%

101 rated

Answer

To calculate the kinetic energy of an electron moving at $0.95c$ , we first need the rest mass energy of the electron, which can be given by:

$E_0 = mc^2 = (9.11 \times 10^{-31} \, kg)(3.00 \times 10^8 \, m/s)^2 = 8.187 \times 10^{-14} \, J$

Using the formula for relativistic kinetic energy:

$E_k = \left( \frac{m v}{\sqrt{1 - \frac{v^2}{c^2}}} - mc^2\right)$

Substituting $v = 0.95c$ :

Calculate the Lorentz factor:

$\gamma = \frac{1}{\sqrt{1 - (0.95)^2}} = 2.99$
Kinetic energy can then be computed as:

$E_k = (\gamma - 1) mc^2 = (2.99 - 1) (9.11 \times 10^{-31})(3.00 \times 10^8)^2 = 1.43 \times 10^{-13} \, J$

Thus, the kinetic energy of one electron travelling at a speed of $0.95c$ is approximately $1.43 \times 10^{-13} \, J$ .

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Deduce whether the data in Table 1 are consistent with this prediction.

Discuss how Einstein's theory of special relativity explains the data in Table 1.

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Join the A-Level students using SimpleStudy...