Photo AI
Figure 9 shows some of the apparatus used in a demonstration of electrical power transmission using a dc power supply - AQA - A-Level Physics - Question 5 - 2020 - Paper 1
Question 5
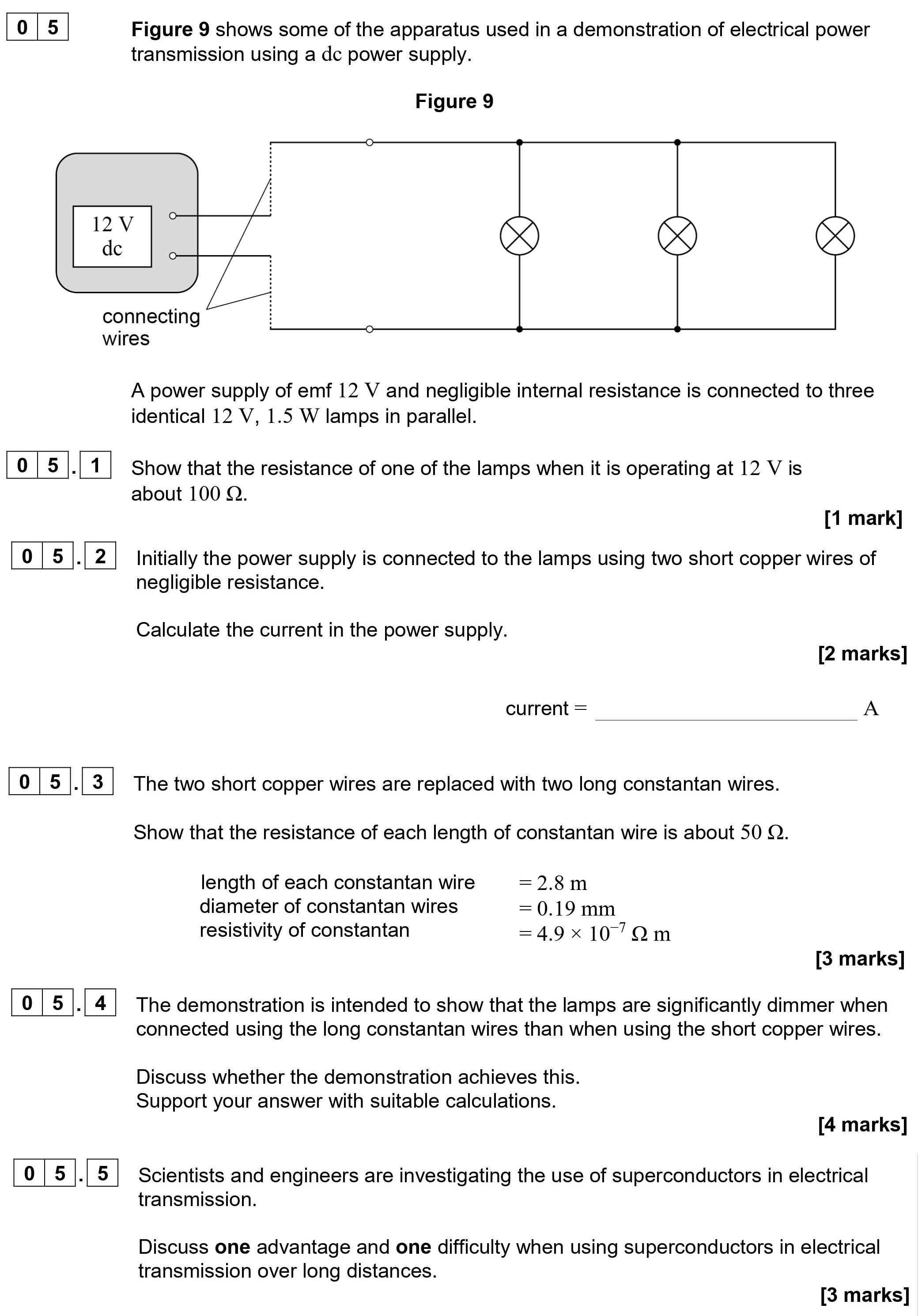
Figure 9 shows some of the apparatus used in a demonstration of electrical power transmission using a dc power supply. A power supply of emf 12 V and negligible int... show full transcript
Worked Solution & Example Answer:Figure 9 shows some of the apparatus used in a demonstration of electrical power transmission using a dc power supply - AQA - A-Level Physics - Question 5 - 2020 - Paper 1
Step 1
5.1 Show that the resistance of one of the lamps when it is operating at 12 V is about 100 Ω.
Answer
To find the resistance of one lamp, we can use the power formula:
P = rac{V^2}{R}
Rearranging gives:
R = rac{V^2}{P}
Substituting the known values:
R = rac{(12 ext{ V})^2}{1.5 ext{ W}} = rac{144}{1.5} = 96 ext{ Ω}
This value approximates to about 100 Ω.
Step 2
5.2 Calculate the current in the power supply.
Answer
First, calculate the total resistance of the lamps in parallel. The resistance of one lamp is approximately 100 Ω, so:
R_{total} = rac{1}{ rac{1}{R_1} + rac{1}{R_2} + rac{1}{R_3}} = rac{1}{ rac{1}{100} + rac{1}{100} + rac{1}{100}} = rac{1}{ rac{3}{100}} = rac{100}{3} ext{ Ω} \\ \\ R_{total} ext{ is approximately } 33.33 ext{ Ω.}
Using Ohm’s law, where I = rac{V}{R}:
I = rac{12 ext{ V}}{33.33 ext{ Ω}} \\ \\ I ext{ is approximately } 0.36 ext{ A.}
Step 3
5.3 Show that the resistance of each length of constantan wire is about 50 Ω.
Answer
Using the formula for resistance:
ho rac{L}{A}$$ Where: - $R$ = resistance - $ ho$ = resistivity of constantan = $4.9 imes 10^{-7} ext{ Ω m}$ - $L$ = length of each wire = 2.8 m - $A$ = cross-sectional area = $ rac{ ext{π}(d/2)^2}{4} = rac{ ext{π}( rac{0.19 ext{ mm}}{2})^2}{4}$ Converting to meters: - $d = 0.19 ext{ mm} = 0.19 imes 10^{-3} ext{ m}$ - Thus, calculate $A$: $$A ext{ (in m}^2 ext{)} = rac{ ext{π}(0.19 imes 10^{-3}/2)^2}{4} \\ \\ R ext{ evaluates to about } 50 ext{ Ω.}$$Step 4
5.4 Discuss whether the demonstration achieves this.
Answer
The use of long constantan wires increases the resistance in the circuit compared to short copper wires, causing a decrease in current. According to Ohm's law, the current through the lamps would be:
I = rac{V}{R}
The increase in resistance leads to a lower current, which results in dimmer lamps. By calculating the total resistance with the longer wires, it can be shown that the lamps would receive less voltage, thus appearing dimmer. Therefore, the demonstration successfully shows the effects of higher resistance due to wire length on lamp brightness.
Step 5
5.5 Discuss one advantage and one difficulty when using superconductors in electrical transmission over long distances.
Answer
Advantage
One major advantage of using superconductors is that they exhibit zero resistivity, which leads to no energy loss during transmission. This significantly enhances efficiency in electrical power transmission over long distances, reducing costs associated with energy loss.
Difficulty
However, a critical difficulty is maintaining the superconductors at very low temperatures, which is necessary for them to function. This requirement often involves advanced cooling technology, which can be costly and complex to implement, limiting the practical applications of superconductors.
