Photo AI
Charged plates X and Y have a potential difference 1.5 V between them - AQA - A-Level Physics - Question 22 - 2019 - Paper 1
Question 22
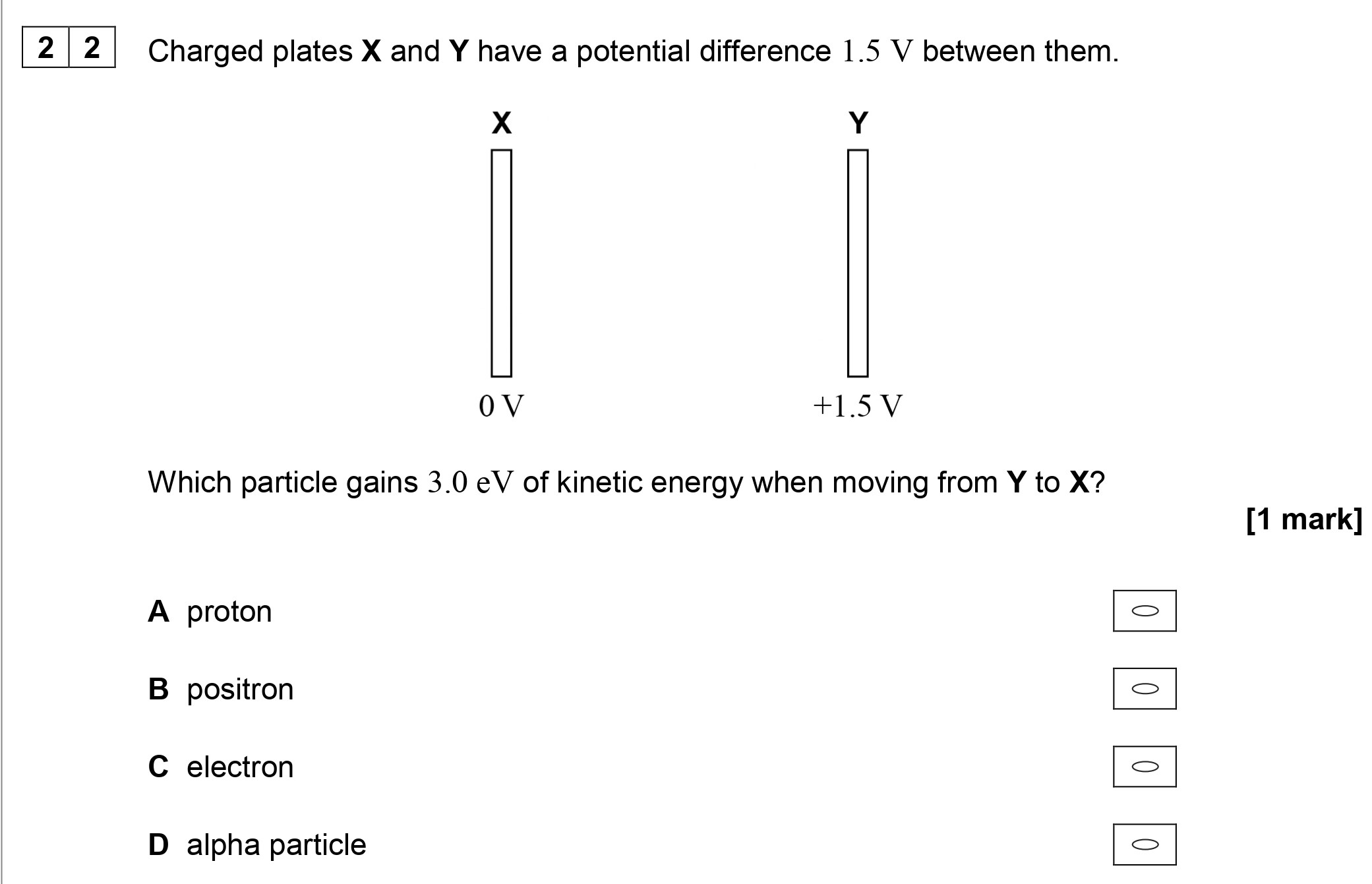
Charged plates X and Y have a potential difference 1.5 V between them. Which particle gains 3.0 eV of kinetic energy when moving from Y to X? A proton B positron C... show full transcript
Worked Solution & Example Answer:Charged plates X and Y have a potential difference 1.5 V between them - AQA - A-Level Physics - Question 22 - 2019 - Paper 1
Step 1
Which particle gains 3.0 eV of kinetic energy when moving from Y to X?
Answer
To determine which particle gains 3.0 eV of kinetic energy moving from plate Y (+1.5 V) to plate X (0 V), we start with the relationship between potential difference and kinetic energy:
The change in potential energy (which is equal to the kinetic energy gained by the particle) can be calculated using the formula:
where:
- is the kinetic energy gained,
- is the charge of the particle, and
- is the potential difference.
Since the potential difference is 1.5 V, a particle would gain:
- A proton (charge e): For this particle, the kinetic energy gained would be:
- A positron (charge e): Similar to the proton,
- An electron (charge -e): The kinetic energy gained when moving towards a lower potential is:
- An alpha particle (charge 2e): Therefore, the kinetic energy for an alpha particle would be:
Thus, the particle that gains 3.0 eV of kinetic energy when moving from Y to X is the alpha particle (D).
