Photo AI
Horizontal escape lanes made of loose gravel have been constructed at the side of some roads on steep hills so that vehicles can stop safely when their brakes fail - AQA - A-Level Physics - Question 1 - 2018 - Paper 1
Question 1
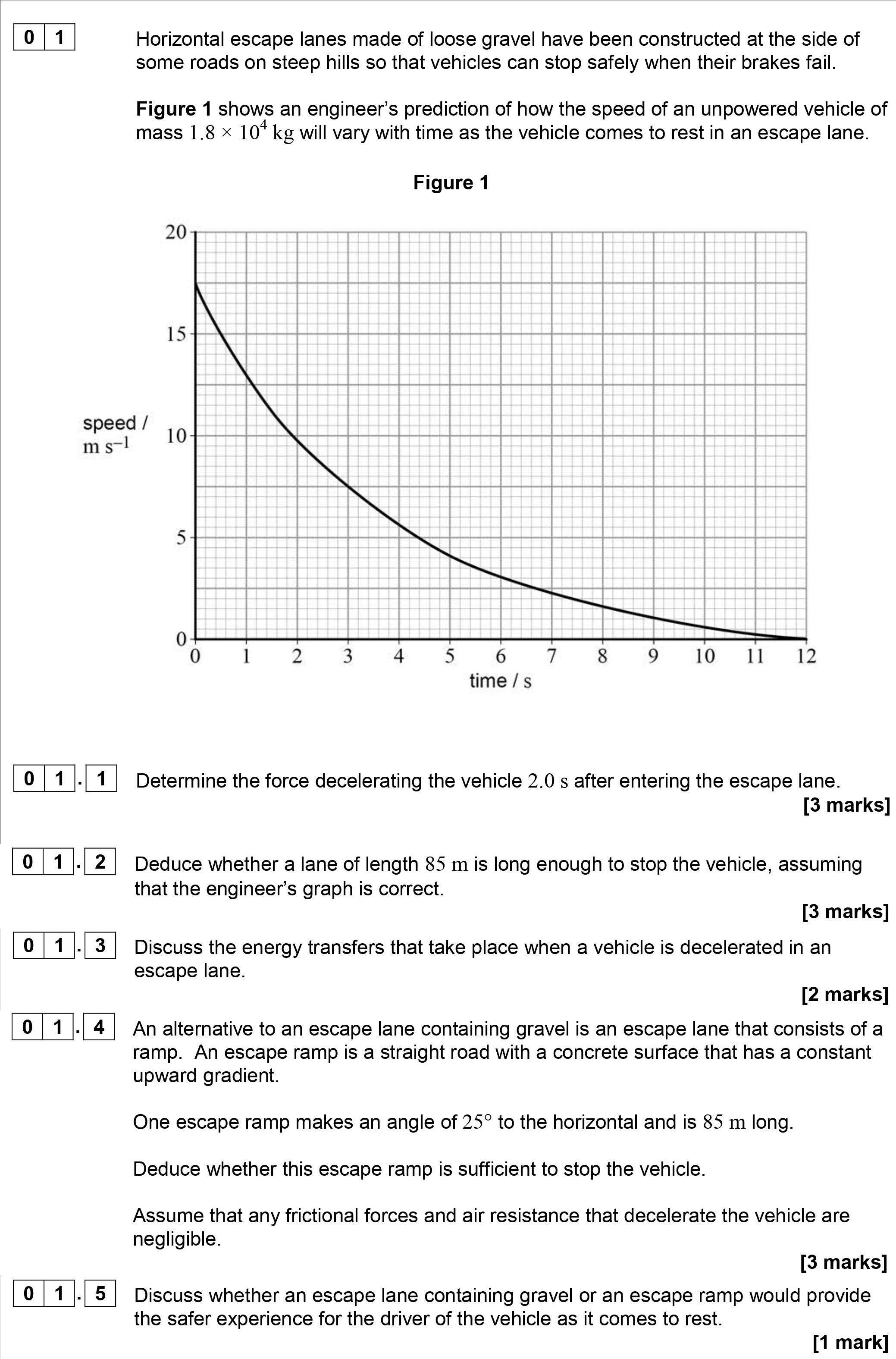
Horizontal escape lanes made of loose gravel have been constructed at the side of some roads on steep hills so that vehicles can stop safely when their brakes fail. ... show full transcript
Worked Solution & Example Answer:Horizontal escape lanes made of loose gravel have been constructed at the side of some roads on steep hills so that vehicles can stop safely when their brakes fail - AQA - A-Level Physics - Question 1 - 2018 - Paper 1
Step 1
Determine the force decelerating the vehicle 2.0 s after entering the escape lane.
Answer
To find the force decelerating the vehicle, we first need to determine the deceleration at 2.0 s using the graph. A tangent can be drawn at the point corresponding to t = 2.0 s, yielding a speed of approximately 15 m/s at that moment. The graph shows a slowdown of 0 to 15 m/s over 2 s, leading to a deceleration Next, we use Newton's second law (F = ma) to find the force: Thus, the force decelerating the vehicle is approximately -1.35 x 10^7 N.
Step 2
Deduce whether a lane of length 85 m is long enough to stop the vehicle, assuming that the engineer's graph is correct.
Answer
Using the formula for distance covered under uniform acceleration: In this case, initial speed (u) at t = 0 is 20 m/s, a = -7.5 m/s² (as calculated before), and t can be computed based on when the vehicle comes to rest. The stopping time can be calculated with: Substituting into the distance formula: The total distance of 25.1 m is much less than the 85 m lane, thus the lane is long enough.
Step 3
Discuss the energy transfers that take place when a vehicle is decelerated in an escape lane.
Answer
When a vehicle decelerates, its kinetic energy is transferred into other forms of energy. Initially, the vehicle possesses kinetic energy given by: As the vehicle comes to a stop, this kinetic energy is converted mainly into heat energy due to friction between the tires and the gravel. Some energy may also be transferred to the surrounding environment, raising the temperature of the gravel. Additionally, some work is done against any resistance, including air resistance, although it is negligible in this scenario.
Step 4
Deduce whether this escape ramp is sufficient to stop the vehicle.
Answer
To analyze the escape ramp, we find its height using trigonometry: Let the length of the ramp be 85 m and angle be 25°. Then, we calculate the potential energy at the top of the ramp: Next, we equate this potential energy with the kinetic energy at the start: As the potential energy exceeds the kinetic energy, the ramp is sufficient to stop the vehicle.
Step 5
Discuss whether an escape lane containing gravel or an escape ramp would provide the safer experience for the driver of the vehicle as it comes to rest.
Answer
The safety of an escape lane versus an escape ramp largely depends on the conditions of use. An escape lane of gravel provides a more effective surface for friction, allowing for a quicker deceleration and preventing the risk of rolling back. On the other hand, an escape ramp, while theoretically effective due to potential energy conversion, could become dangerous if the angle is too steep or if the vehicle does not have sufficient speed to navigate the incline safely. If the vehicle comes to rest on a ramp, there is also a higher chance of rolling back down due to gravity if it's not entirely stopped. Thus, for ensuring better safety upon abrupt stops, a gravel escape lane would generally provide a safer experience.
