Photo AI
Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7
Question 4
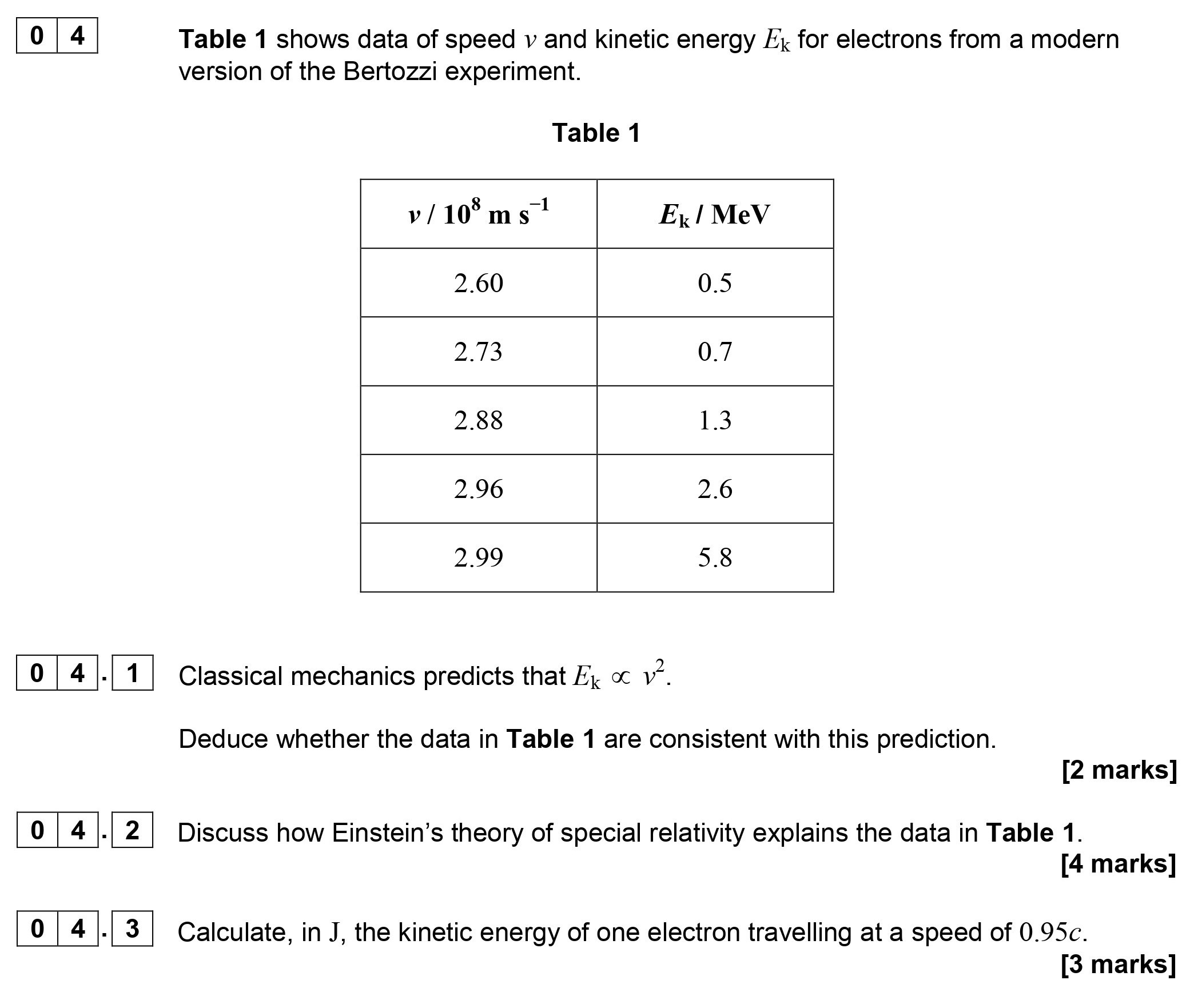
Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. Table 1 | $v / 10^8 \, \mathrm{m \, s^{-1}... show full transcript
Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7
Step 1
Deduce whether the data in Table 1 is consistent with this prediction.
Answer
To determine if the data is consistent with the prediction that , we can analyze at least two data points from the table and compute the ratio of to for these values:
-
For ,
Therefore,
-
For ,
Therefore,
Since both calculations yield similar constants, we can conclude that the data in Table 1 is consistent with the prediction that .
Step 2
Discuss how Einstein’s theory of special relativity explains the data in Table 1.
Answer
Einstein's theory of special relativity introduces the concept of relativistic mass, which changes as an object approaches the speed of light, . As velocity increases, so does the kinetic energy, following the relation:
where is the Lorentz factor and is the rest mass. For low speeds, this leads to the classical approximation , but as approaches , the increase in kinetic energy becomes nonlinear.
In the data from Table 1, we see kinetic energies that don’t align with classical predictions as the speeds increase. For example, at , the kinetic energy vastly exceeds what would be predicted classically, demonstrating the need for relativistic considerations. Einstein's theory effectively accounts for the differences, illustrating that at high velocities, mass and energy behave in ways that classical mechanics cannot accurately describe.
Step 3
Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.
Answer
To calculate the kinetic energy of one electron travelling at 0.95c, we again use the relation from Einstein's theory:
-
First, calculate the rest mass energy of the electron:
- The rest mass of an electron is approximately . Thus,
- The rest mass of an electron is approximately . Thus,
-
Next, calculate the Lorentz factor for :
-
Finally, using these values:
Thus, the kinetic energy of one electron travelling at a speed of 0.95c is approximately .
