Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. Table 1 | $v / 10^8 \mathrm{ m \ s^{-1}}$ | $E_k / \mathrm{MeV}$ | |-------------------|----------| | 2.60 | 0.5 | | 2.73 | 0.7 | | 2.88 | 1.3 | | 2.96 | 2.6 | | 2.99 | 5.8 | Classical mechanics predicts that $E_k \propto v^2$. 1.1 Deduce whether the data in Table 1 are consistent with this prediction. 1.2 Discuss how Einstein’s theory of special relativity explains the data in Table 1. 1.3 Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Photo AI

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Question 4

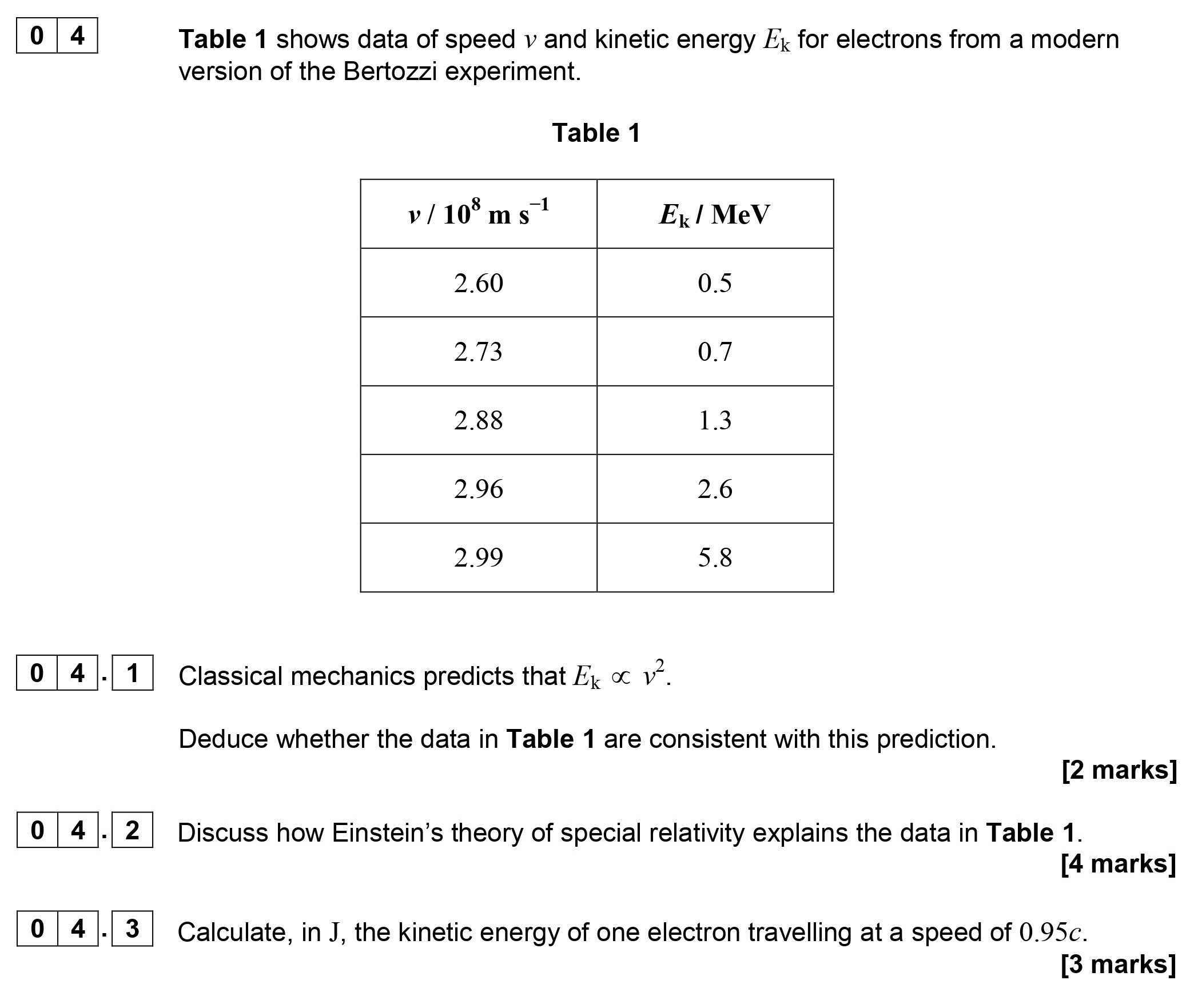
Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. Table 1 | $v / 10^8 \mathrm{ m \ s^{-1}}$ ... show full transcript

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Step 1

Deduce whether the data in Table 1 are consistent with this prediction.

96%

114 rated

Answer

To determine if the data support the prediction that kinetic energy $E_k \propto v^2$ , we will consider the ratio of $E_k$ to $v^2$ for at least two sets of data from Table 1.

Calculating:

For $v = 2.60 \times 10^8 \mathrm{m \ s^{-1}}$ :
- $E_k = 0.5 \mathrm{MeV} = 0.5 \times 1.6 \times 10^{-13} \mathrm{J} \approx 8.0 \times 10^{-14} \mathrm{J}$ .
- $v^2 = (2.60 \times 10^8)^2 \approx 6.76 \times 10^{16} \mathrm{m^2 \ s^{-2}}$ .
- Thus, the ratio $rac{E_k}{v^2} \approx \frac{8.0 \times 10^{-14}}{6.76 \times 10^{16}} \approx 1.18 \times 10^{-30}$ .
For $v = 2.99 \times 10^8 \mathrm{m \ s^{-1}}$ :
- $E_k = 5.8 \mathrm{MeV} \approx 9.28 \times 10^{-13} \mathrm{J}$ .
- $v^2 = (2.99 \times 10^8)^2 \approx 8.94 \times 10^{16} \mathrm{m^2 \ s^{-2}}$ .
- Thus, the ratio $rac{E_k}{v^2} \approx \frac{9.28 \times 10^{-13}}{8.94 \times 10^{16}} \approx 1.04 \times 10^{-29}$ .

Since these ratios decrease with increasing $v$ , the data suggest that the relationship between $E_k$ and $v^2$ may not be direct due to relativistic effects as speeds approach the speed of light.

Step 2

Discuss how Einstein’s theory of special relativity explains the data in Table 1.

99%

104 rated

Answer

Einstein’s theory of special relativity posits that as particles like electrons accelerate to speeds close to the speed of light, their mass effectively increases, which in turn affects their kinetic energy.

As per special relativity, the relativistic kinetic energy $E_k$ can be described by the formula: $E_k = (\gamma - 1) m_0 c^2$ where $\gamma = \frac{1}{\sqrt{1 - (v^2 / c^2)}}$ and $m_0$ is the rest mass of the electron.

As the velocity $v$ of the electron approaches the speed of light $c$ , $\gamma$ increases significantly, and thus the kinetic energy $E_k$ increases disproportionately compared to classical predictions. This explains why the data in Table 1 shows kinetic energy that does not align with the classical $v^2$ relationship, instead indicating a more complex relationship dictated by relativistic effects.

Step 3

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

96%

101 rated

Answer

To calculate the kinetic energy for an electron travelling at a speed of $0.95c$ , we first find $\gamma$ : $\gamma = \frac{1}{\sqrt{1 - (0.95)^2}} \approx 2.83.$

Using the rest mass of the electron, $m_0 \approx 9.11 \times 10^{-31} \mathrm{kg}$ , the kinetic energy is given by: $E_k = (\gamma - 1) m_0 c^2$ Substituting the known values, $E_k = (2.83 - 1)(9.11 \times 10^{-31} \mathrm{kg})(3.00 \times 10^8 \mathrm{m \ s^{-1}})^2$ $E_k = 1.83 \times (9.11 \times 10^{-31})(9.00 \times 10^{16})\approx 1.50 \times 10^{-14} ext{ J}.$

Thus, the kinetic energy of one electron travelling at a speed of 0.95c is approximately $1.50 \times 10^{-14}$ J.

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Deduce whether the data in Table 1 are consistent with this prediction.

Discuss how Einstein’s theory of special relativity explains the data in Table 1.

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Join the A-Level students using SimpleStudy...