Photo AI
There is an analogy between quantities in rotational and translational dynamics - AQA - A-Level Physics - Question 1 - 2017 - Paper 6
Question 1
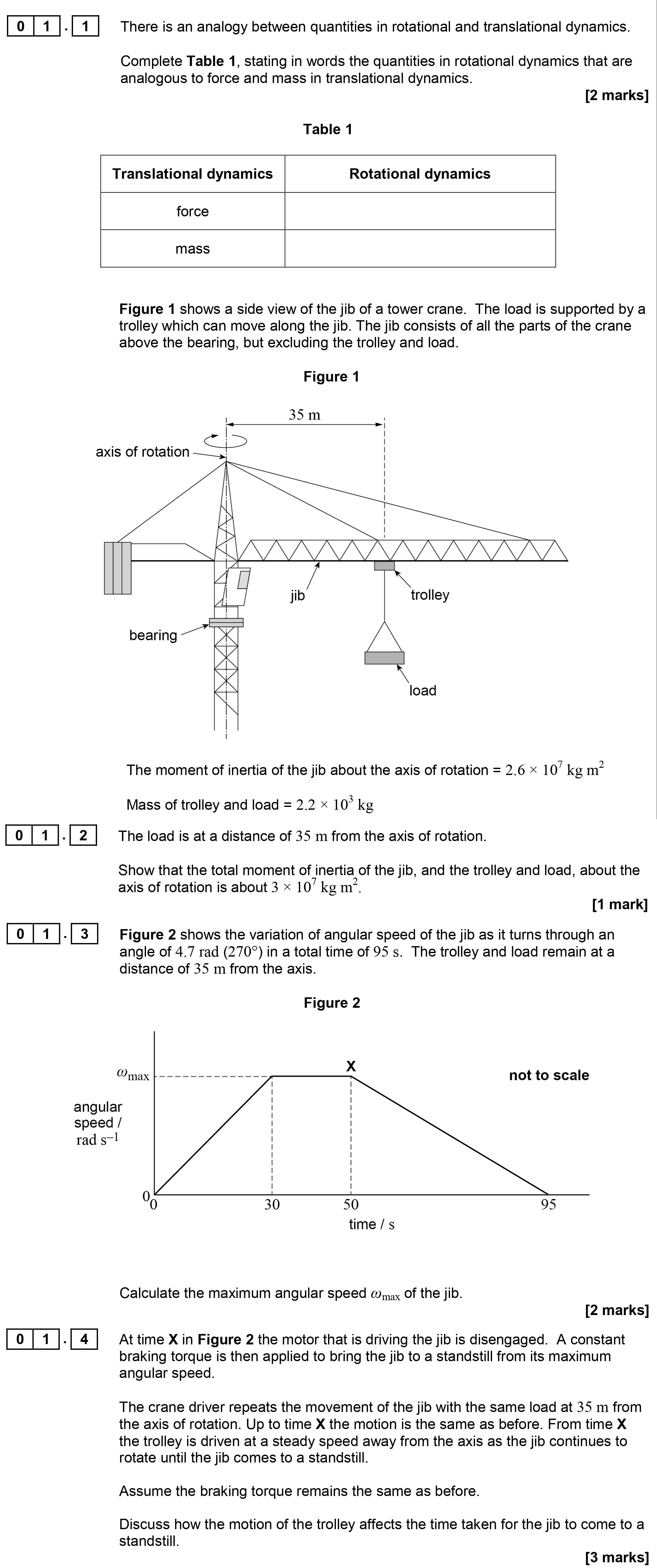
There is an analogy between quantities in rotational and translational dynamics. Complete Table 1, stating in words the quantities in rotational dynamics that are a... show full transcript
Worked Solution & Example Answer:There is an analogy between quantities in rotational and translational dynamics - AQA - A-Level Physics - Question 1 - 2017 - Paper 6
Step 1
Step 2
Show total moment of inertia
Answer
To find the total moment of inertia, we add the moment of inertia of the jib and the contributions from the trolley and load.
Using the formula: where:
- (mass of trolley and load)
- (distance from the axis of rotation)
Calculating the contribution:
Finally, summing:
This confirms that the total moment of inertia is approximately .
