Photo AI
There is an analogy between quantities in rotational and translational dynamics - AQA - A-Level Physics - Question 1 - 2017 - Paper 6
Question 1
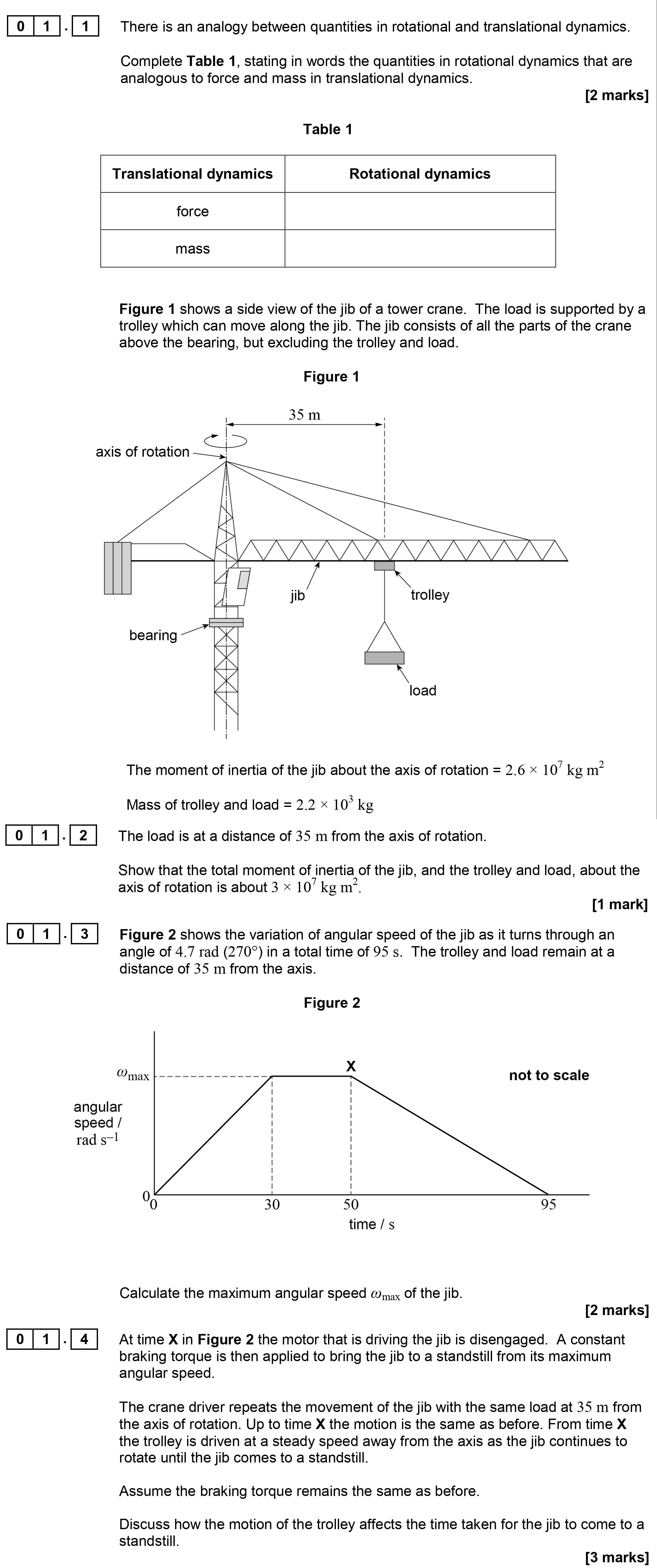
There is an analogy between quantities in rotational and translational dynamics. Complete Table 1, stating in words the quantities in rotational dynamics that are a... show full transcript
Worked Solution & Example Answer:There is an analogy between quantities in rotational and translational dynamics - AQA - A-Level Physics - Question 1 - 2017 - Paper 6
Step 1
Complete Table 1 with the analogies
Answer
In the context of translational dynamics, the quantities that are analogous to force and mass in rotational dynamics are:
- Force corresponds to Torque in rotational dynamics, representing the rotational equivalent of linear force applied to an object.
- Mass corresponds to Moment of Inertia, which is the rotational equivalent of mass that quantifies an object's resistance to changes in its rotational motion.
Step 2
Show total moment of inertia
Answer
To find the total moment of inertia about the axis of rotation, we sum the moment of inertia of the jib and the contributions from the trolley and load:
-
Moment of inertia of the jib:
-
Moment of inertia of the trolley:
-
Moment of inertia of the load: Assuming the load has the same mass as the trolley, we calculate the same way:
-
Total moment of inertia:
Step 3
Calculate the maximum angular speed ω_max
Answer
To calculate the maximum angular speed of the jib, we use the area under the angular speed versus time graph:
-
The total area under the graph represents the angular displacement, which can be represented as: ext{Angular displacement} = rac{1}{2} imes ext{height} imes ext{base}
-
The area consists of two triangles:
- First triangle (0 to 50 s): ext{Area}_{1} = rac{1}{2} imes 50 ext{ s} imes ext{max height}
- Second triangle (50 to 95 s): ext{Area}_{2} = rac{1}{2} imes (95-50) ext{ s} imes ext{max height}
-
Thus, the total area giving angular displacement is: heta = ( rac{1}{2} imes 50 imes ext{ω}_{max}) + ( rac{1}{2} imes 45 imes ext{ω}_{max}) = 4.7 ext{ rad}
-
Solving for ω_max: ext{ω}_{max} = rac{2 imes 4.7}{50 + 45} = rac{9.4}{95} ext{ rad/s} ext{ yielding } 0.099 ext{ rad/s}
Step 4
Calculate the time for the jib to come to a standstill after braking
Answer
When the motor is disengaged and a constant braking torque is applied, the total moment of inertia increases due to the trolley moving outward.
Using the relationship between angular deceleration and torque, let:
- Torque = moment of inertia × angular deceleration
Given that the braking torque remains constant, the time taken can be determined:
-
Assume it takes seconds to stop:
- The equation becomes:
-
Since the final angular speed is zero, we find: T = rac{ ext{ω}_{max}}{ ext{angular deceleration}}
Using the values calculated previously, you can substitute to find the exact stopping time for the jib.
